Polarform komplexer Zahlen

Darstellung in Polarkoordinaten: Betrag und Argument

Neben der Normalform z = a + bi gibt es eine zweite wichtige Darstellung komplexer Zahlen: die Polarform. Sie nutzt den Betrag (Länge) und das Argument (Winkel) zur Beschreibung einer komplexen Zahl.

Die Polarform ist besonders nützlich für Multiplikation, Division und höhere Potenzen komplexer Zahlen.

Grundkonzept der Polarform

In der Gaußschen Zahlenebene kann jede komplexe Zahl als Vektor vom Ursprung zu ihrem entsprechenden Punkt dargestellt werden. Dieser Vektor ist eindeutig bestimmt durch:

Betrag r

Die Länge des Vektors

r = |z| = √(a² + b²)

Abstand vom Ursprung

Argument φ

Der Winkel zur positiven reellen Achse

φ = arg(z) = arctan(b/a)

Winkel im Bogenmaß oder Grad

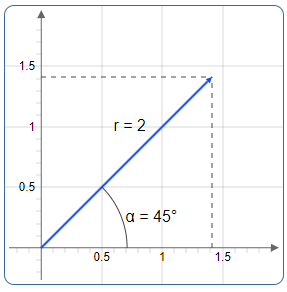
Polarform: Betrag und Argument

Abbildung 1: Polarkoordinaten: Betrag r = 2 und Winkel φ = 45°

Winkelkonvention

Winkelrichtung:
  • Positive Winkel: Gegen den Uhrzeigersinn (von der positiven reellen Achse)
  • Negative Winkel: Im Uhrzeigersinn
  • Bereich: Normalerweise -π < φ ≤ π (oder -180° < φ ≤ 180°)
  • Alternative: Auch 0 ≤ φ < 2π (oder 0° ≤ φ < 360°) wird verwendet

Definition der Polarform

Polarform einer komplexen Zahl:

z = r · e^(iφ) = r(cos φ + i sin φ)

wobei:
r = |z| = Betrag (Modulus)
φ = arg(z) = Argument (Winkel)

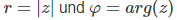
Polarform Notation

Euler'sche Formel

Die Euler'sche Formel verbindet die trigonometrische und exponentielle Form:

e^(iφ) = cos φ + i sin φ

Dies ist eine der wichtigsten Formeln in der Mathematik!

Exponentielle Form

z = r·e^(iφ)

Kompakte Schreibweise

Trigonometrische Form

z = r(cos φ + i sin φ)

Mit Cosinus und Sinus

Umwandlung: Normalform → Polarform

Berechnung des Betrags

Der Betrag einer komplexen Zahl z = a + bi wird nach dem Satz des Pythagoras berechnet:

r = |z| = √(a² + b²)

Berechnung des Arguments

Das Argument ist der Winkel φ, den der Vektor mit der positiven reellen Achse einschließt:

φ = arctan(b/a)

WICHTIG: Der Quadrant muss beachtet werden!

Achtung vor Quadranten:

Die Funktion arctan gibt nur Winkel zwischen -π/2 und π/2 zurück. Je nach Quadrant muss π addiert oder subtrahiert werden:

  • Quadrant I (a > 0, b > 0): φ = arctan(b/a)
  • Quadrant II (a < 0, b > 0): φ = π + arctan(b/a)
  • Quadrant III (a < 0, b < 0): φ = -π + arctan(b/a)
  • Quadrant IV (a > 0, b < 0): φ = arctan(b/a)

Beispiel 1: z = 3 + 3i

Gegeben: z = 3 + 3i → a = 3, b = 3
Betrag: r = √(3² + 3²) = √18 = 3√2 ≈ 4,243
Argument: tan(φ) = 3/3 = 1
Quadrant: I (a > 0, b > 0)
Winkel: φ = arctan(1) = π/4 = 45°
Polarform: z = 3√2 · e^(i·π/4) oder z = 3√2(cos 45° + i sin 45°)

Beispiel 2: z = -2 + 2i

Gegeben: z = -2 + 2i → a = -2, b = 2
Betrag: r = √((-2)² + 2²) = √8 = 2√2 ≈ 2,828
Argument: tan(φ) = 2/(-2) = -1
Quadrant: II (a < 0, b > 0)
Winkel: φ = π - π/4 = 3π/4 = 135°
Polarform: z = 2√2 · e^(i·3π/4)

Umwandlung: Polarform → Normalform

Um von der Polarform zurück zur Normalform zu gelangen, nutzen wir die trigonometrischen Funktionen:

Rücktransformation:

z = r(cos φ + i sin φ) = r cos φ + i r sin φ

Also: a = r cos φ und b = r sin φ

Beispiel: z = 2·e^(i·π/3)

Gegeben: z = 2·e^(i·π/3) → r = 2, φ = π/3 = 60°
Realteil: a = r cos φ = 2 cos(60°) = 2 · 0,5 = 1
Imaginärteil: b = r sin φ = 2 sin(60°) = 2 · (√3/2) = √3 ≈ 1,732
Normalform: z = 1 + √3·i

Vergleich: Normalform vs. Polarform

Aspekt Normalform (a + bi) Polarform (r·e^(iφ))
Schreibweise z = a + bi z = r·e^(iφ) oder r(cos φ + i sin φ)
Komponenten Realteil a, Imaginärteil b Betrag r, Argument φ
Addition/Subtraktion Einfach (komponentenweise) Kompliziert
Multiplikation Kompliziert (ausmultiplizieren) Einfach (r multiplizieren, φ addieren)
Division Kompliziert (mit konjugierter erweitern) Einfach (r dividieren, φ subtrahieren)
Potenzen Sehr kompliziert Einfach (Moivre-Formel)
Fazit:

Normalform ist besser für Addition/Subtraktion. Polarform ist besser für Multiplikation/Division/Potenzen.

Praktische Anwendungen

Elektrotechnik: Wechselstrom

  • Phasoren: Spannungen und Ströme als komplexe Zahlen in Polarform
  • Impedanz: Z = |Z|·e^(iφ) mit Betrag und Phasenversatz
  • Resonanz: Analyse durch Argument (Phasenverhältnis)

Signalverarbeitung

  • Fourier-Analyse: Spektrum in Magnitude (Betrag) und Phase (Argument)
  • Filter: Frequenzgang durch r(ω) und φ(ω)

Rotationen und Transformationen

  • Drehung: Multiplikation mit e^(iα) dreht um Winkel α
  • Skalierung: Multiplikation mit r ändert die Länge
  • Grafik: 2D-Transformationen durch komplexe Arithmetik

Zusammenfassung und Übersicht

Konzept Formel Bedeutung
Betrag r = √(a² + b²) Abstand vom Ursprung in der Gaußschen Ebene
Argument φ = arctan(b/a) Winkel zur positiven reellen Achse
Polar → Normal a = r cos φ, b = r sin φ Umwandlung in Komponenten
Normal → Polar r = √(a² + b²), φ = arctan(b/a) Umwandlung in Betrag und Winkel
Euler'sche Formel e^(iφ) = cos φ + i sin φ Verbindung Exponentialfunktion und Trigonometrie

Tipps und häufige Fehler

Tipps zum Arbeiten mit Polarform:
  • Quadranten beachten: atan allein reicht nicht, Quadrant überprüfen
  • Winkelmaß konsistent: Alle Winkel in Grad oder Radiant
  • Betrag immer positiv: r > 0 immer
  • Winkelperiodizität: φ und φ + 2π geben die gleiche Zahl
  • Euler'sche Formel merken: e^(iφ) = cos φ + i sin φ
Häufige Fehler:
  • FALSCH: φ = arctan(b/a) ohne Quadrantbeachtung | RICHTIG: Quadrant überprüfen!
  • FALSCH: Radius kann negativ sein | RICHTIG: r = |z| ≥ 0 immer
  • FALSCH: e^(iφ) = sin φ + i cos φ | RICHTIG: e^(iφ) = cos φ + i sin φ
  • FALSCH: Degree und Radiant vermischen | RICHTIG: Konsistentes Winkelmaß verwenden


























Ist diese Seite hilfreich?            
Vielen Dank für Ihr Feedback!

Das tut uns leid

Wie können wir die Seite verbessern?