Multiplikation und Division in Polarform
Einfache Operationen mit Betrag und Winkel statt Komponenten
Die Polarform hat einen großen Vorteil: Die Multiplikation und Division werden deutlich einfacher als in Normalform! Statt aufwendiges Ausmultiplizieren oder Erweitern mit der Konjugierten müssen wir nur Beträge multiplizieren/dividieren und Winkel addieren/subtrahieren.
Dies ist einer der Hauptgründe, warum die Polarform in der Praxis so wichtig ist.
Multiplikation in Polarform
Das Konzept: Beträge multiplizieren, Winkel addieren
Bei der Multiplikation zweier komplexer Zahlen in Polarform gilt eine elegante Regel:
z₁ · z₂ = r₁·r₂ · e^(i(φ₁ + φ₂))
In Worte:
Beträge multiplizieren: |z₁ · z₂| = |z₁| · |z₂|
Winkel addieren: arg(z₁ · z₂) = arg(z₁) + arg(z₂)

Geometrische Interpretation
Geometrisch bedeutet die Multiplikation:
Skalierung
Der Vektor wird um den Faktor r₂ gestreckt oder gestaucht
|z₂| > 1: Verlängerung
|z₂| < 1: Verkürzung
Rotation
Der Vektor wird um den Winkel φ₂ gegen den Uhrzeigersinn gedreht
φ₂ > 0: Gegenuhrzeiger
φ₂ < 0: Im Uhrzeiger
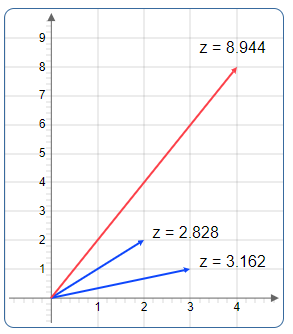
Abbildung 1: Geometrische Darstellung der Multiplikation
Beispiel 1: z₁ = 3·e^(i·30°) und z₂ = 2·e^(i·45°)
Beispiel 2: z₁ = 5·e^(i·60°) und z₂ = 2·e^(i·120°)
Beispiel 3: Mit negativem Winkel
Division in Polarform
Das Konzept: Beträge dividieren, Winkel subtrahieren
Ähnlich wie bei der Multiplikation ist auch die Division in Polarform elegant:
z₁ / z₂ = (r₁/r₂) · e^(i(φ₁ - φ₂))
In Worte:
Beträge dividieren: |z₁ / z₂| = |z₁| / |z₂|
Winkel subtrahieren: arg(z₁ / z₂) = arg(z₁) - arg(z₂)
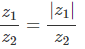
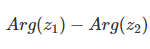
Beispiel 1: z₁ = 12·e^(i·75°) und z₂ = 4·e^(i·30°)
Beispiel 2: z₁ = 10·e^(i·180°) und z₂ = 2·e^(i·90°)
Vergleich: Normalform vs. Polarform
Die Vorteile der Polarform werden bei Multiplikation und Division besonders deutlich:
| Operation | In Normalform | In Polarform |
|---|---|---|
| Multiplikation | Ausmultiplizieren aller Terme, i² ersetzen, Zusammenfassen | Beträge multiplizieren, Winkel addieren |
| Division | Mit Konjugierter erweitern, ausmultiplizieren, vereinfachen | Beträge dividieren, Winkel subtrahieren |
| Komplexität | Sehr aufwändig | Sehr einfach |
| Rechenaufwand | Mehrere Schritte | Ein bis zwei Schritte |
Für Multiplikation und Division ist die Polarform eindeutig überlegen. Deshalb wird in der Praxis oft in Polarform umgerechnet, die Operation durchgeführt, und dann zurück in Normalform konvertiert, falls nötig.
Bonus: Potenzen in Polarform (Moivre-Formel)
Ein großer Vorteil der Polarform: Die Moivre-Formel macht auch Potenzen einfach zu berechnen!
z^n = r^n · e^(i·n·φ)
In Worte: Betrag zur Potenz n, Winkel mit n multiplizieren
Beispiel: (2·e^(i·30°))³
- Betrag: 2³ = 8
- Winkel: 3 · 30° = 90°
- Resultat: z³ = 8·e^(i·90°) = 8i
Praktische Anwendungen
Elektrotechnik: AC-Schaltungen
- Impedanz-Berechnung: Z₁ · Z₂ durch Multiplikation der Phasoren
- Leistungsfluss: Schnelle Berechnung über Polarform
Signalverarbeitung
- Filter: Frequenzgang durch Multiplikation/Division
- Phase und Magnitude: Getrennte Behandlung durch Polarform
Mechanik und Ingenieurwesen
- Vibration: Schwingungen als komplexe Größen
- Rotationen: Multiplikation mit e^(iφ) = Drehung um φ
Zusammenfassung und Algorithmus
| Operation | Betrag | Winkel | Formel |
|---|---|---|---|
| Multiplikation | r = r₁ · r₂ | φ = φ₁ + φ₂ | z₁ · z₂ = r₁r₂ · e^(i(φ₁+φ₂)) |
| Division | r = r₁ / r₂ | φ = φ₁ - φ₂ | z₁ / z₂ = (r₁/r₂) · e^(i(φ₁-φ₂)) |
| Potenz (n) | r = r^n | φ = n · φ | z^n = r^n · e^(i·n·φ) |
Tipps und häufige Fehler
- Werte überprüfen: Ist der Betrag der Lösung r₁·r₂ oder r₁/r₂? ✓
- Winkelbereich kontrollieren: Wenn φ > 360°, dann 360° subtrahieren
- Vorzeichen bei Subtraktion: φ₁ - φ₂ kann negativ sein (das ist OK!)
- Rück-Konvertierung: Wenn Normalform gebraucht, cos/sin verwenden
- Verifikation: Betrag überprüfen: |z₁·z₂| = |z₁|·|z₂| ✓
- FALSCH: Bei Multiplikation Winkel multiplizieren | RICHTIG: Winkel addieren!
- FALSCH: Bei Division Winkel addieren | RICHTIG: Winkel subtrahieren!
- FALSCH: Betrag negativ | RICHTIG: r ≥ 0 immer!
- FALSCH: Winkelbereich ignorieren | RICHTIG: Bei Bedarf normalisieren (0-360° oder -180 bis 180°)
Addition und Subtraktion
Multiplizieren
Konjugieren und Dividieren
Quadratische Gleichungen
Komplexe Zahlen geometrisch darstellen
Geometrische Addition
Betrag (Absoluter Wert)
Polarform
Polarform in Normalform umrechnen
Normalform in Polarform umrechnen
Multiplikation in Polarform
|
|