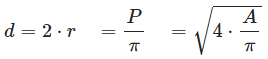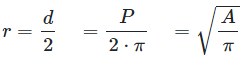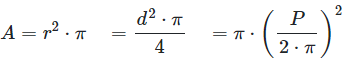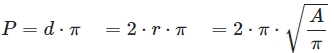Circle
Circle formulas and description
A circle is an endless number of points equidistant from a given point. This given point is the center of the circle.
If you draw a line from the center to any point on the circle, that line is called the radius. Any given circle has an infinite number of radii.
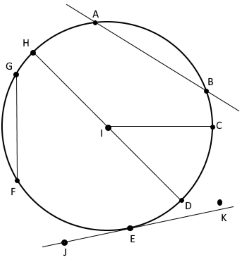
The next figure shows some more segments (chords) and lines related to circles.
-
The center of the circle is the point \(I\)
-
The radius is the segment connecting point \(I\) and point \(C\).
-
The diameter is the segment connecting point \(H\) and point \(D\). The diameter connects two points on the circle and passes through the center. The length is twice the radius
-
The chord is a special type of segment that connects two points of the circle, \(G\) and \(F\). The chord is used to determine a circle segment (circle section). Please read the description of the circle segment.
-
The secant intersects the circle at the points \(A\) and \(B\). Secants are located inside and outside a circle.
-
The tangent \(JK\) is a line that intersects a circle at exactly one point. This intersection is called the tangent point.
Formulas for calculating circles
\(r\) - Radius
\(d\) - diameter
\(P\) - Perimeter
\(A\) - area
Calculate diameter
Calculate radius
Calculate area
Calculate scope
Circle online calculator →
|
|