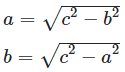Pythagorean Theorem

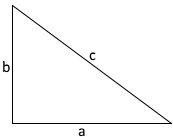
The Pythagorean theorem states that in a right triangle the square of the hypotenuse is equal to the sum of the squares of the sides. The hypotenuse is the longest side of a right triangle. It is always opposite the right angle.

Based on this right triangle, you can write an equation using the Pythagorean theorem as follows:

\(\displaystyle c^2=a^2+b^2\)

From the Pythagorean theorem it can be deduced that the length of the hypotenuse is equal to the square root of the sum of the squares of the legs, i.e

\(\displaystyle c=\sqrt{a^2+b^2}\)

The sides a and b are the lengths of the sides adjacent to the right angle, and the hypotenuse c is the length of the side opposite the right angle.

By rearranging the equation, the third can be calculated from two known sides of a right-angled triangle.

Example

A triangle with a = 3 and b = 4 is calculated.

\(\displaystyle c=\sqrt{a^2+b^2} = \sqrt{3^2+4^2} = \sqrt{9+16}=\sqrt{25}=5\)

Groups of three where a, b and c are each integers are called Pythagorean triples. You can find more information about this at Pythagorean triples

Special right triangles

Two types of right triangles are considered special right triangles. One of the special right triangles has angles of 30°, 60° and 90°. The other special right triangle has angles measuring 45°, 45° and 90°. The size of the triangle doesn't matter; it just needs to have specific measures for its angles.

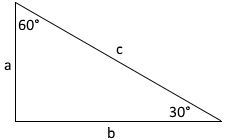
30°, 60° and 90° triangles

The lengths of the sides of a \(30°, 60°, 90°\) triangle are in a ratio of \(b=a·\sqrt{3}\)

The hypotenuse is twice as long as the side \(a\), opposite the \(30°\) angle.

So is \(\displaystyle a = \frac{c}{2}\)  and  \(\displaystyle b= \frac{c}{2}·\sqrt{3}\)

With this information, you can determine the value of a and b for the triangle if you know the value of c.

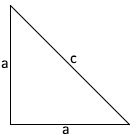
45°, 45° and 90° triangles

The sides \(a\) of a \(45°, 45°, 90° \) triangle are of equal length.

• The ratio of the side lengths to the hypotenuse is \(\displaystyle \frac{1}{\sqrt{2}}\)
• This results in \(\displaystyle a=\frac{c}{\sqrt{2}}\)

The converse of the Pythagorean theorem

You can use the Pythagorean theorem for more than finding side lengths in right triangles. You can also use the Pythagorean theorem to determine whether a triangle is sharp, right, or obtuse. This is known as the converse of the Pythagorean theorem, which reads as follows:

• If \(c^2 < a^2 + b^2\),then the triangle is acute
  
  
• If \(c^2 = a^2 + b^2\), then the triangle is right-angled
  
  
• If \(c^2 > a^2 + b^2\), then the triangle is obtuse

Angle bisector
Median
Altitude and the Orthocenter
Triangle bisector
Pythagorean theorem
Pythagorean triples
Circle
Square
Rectangle
Rhombus
Parallelogram
Trapezoid