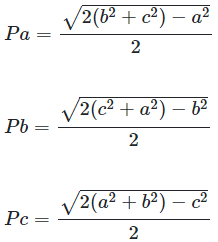Median (geometry)
Description for calculating the bisector of a triangle (median)
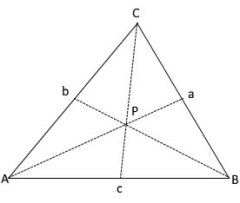
A triangle has different line segments with an intersection. One of the line segments is the median.
-
The median of a triangle is a line segment that connects a vertex to the midpoint of its opposite side
-
Since the median of a triangle can be drawn from any vertex, every triangle has three medians
-
Unlike heights, medians do not form a right angle with the side they intersect
-
A bisectors divides the triangle into two smaller triangles of the same area and height
-
The point of parallelism of the three medians of a triangle is called the center of gravity
-
The center of gravity is always within the triangle and divides the bisector in a ratio of 2:1. The distance from each vertex to the center of gravity of the triangle is twice as long as the distance to the opposite side.
P is the center of mass that divides the medians in a ratio of 2:1
The lengths of the bisectors of the triangle \(a\), \(b\) and \(c\) are calculated using the following formulas
|
|