Kreis
Definition, Eigenschaften und Formeln zur Berechnung von Kreisen
Ein Kreis ist die Menge aller Punkte in einer Ebene, die von einem bestimmten Punkt (dem Mittelpunkt) denselben konstanten Abstand haben. Dieser Abstand heißt Radius.
Der Kreis ist eine der fundamentalsten geometrischen Formen mit wichtigen Anwendungen in Mathematik, Physik, Ingenieurwesen und vielen anderen Bereichen.
Grundelemente des Kreises
Mittelpunkt
Der zentrale Punkt, von dem alle Punkte den gleichen Abstand haben
Radius
Abstand vom Mittelpunkt zu jedem Punkt auf der Kreislinie
Durchmesser
Strecke durch den Mittelpunkt, verbindet zwei Punkte auf der Kreislinie
Umfang
Die Länge der gesamten Kreislinie
- Sehne: Strecke zwischen zwei Punkten auf der Kreislinie
- Sekante: Gerade, die den Kreis an zwei Punkten schneidet
- Tangente: Gerade, die den Kreis genau an einem Punkt berührt
- Bogen: Teil der Kreislinie zwischen zwei Punkten
Kreis - Visualisierung
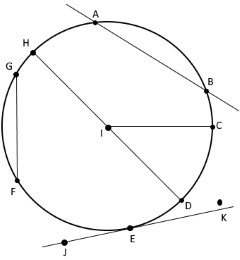
Kreis mit Mittelpunkt, Radius, Durchmesser, Sehne, Sekante und Tangente
Formeln für den Kreis
Für einen Kreis mit Radius \(r\), Durchmesser \(d\), Umfang \(U\) und Fläche \(A\):
Durchmesser
Aus Umfang:
Aus Fläche:
Radius
Aus Umfang:
Aus Fläche:
Umfang
Mit Radius:
Mit Durchmesser:
Aus Fläche:
Flächeninhalt
Mit Radius:
Mit Durchmesser:
Mit Umfang:
Praktische Beispiele
Beispiel 1: Umfang und Fläche mit gegebenem Radius
Gegeben: \(r = 5\,\text{cm}\)
Beispiel 2: Radius aus Fläche berechnen
Gegeben: \(A = 100\,\text{cm}^2\)
Beispiel 3: Durchmesser aus Umfang berechnen
Gegeben: \(U = 50\,\text{cm}\)
Wichtige Eigenschaften
- \(\pi\) (Pi) ist eine mathematische Konstante ≈ 3.14159265...
- Das Verhältnis \(\frac{U}{d} = \pi\) ist für jeden Kreis konstant
- Fläche und Umfang hängen nur vom Radius ab
- Der Kreis ist die Figur mit dem größten Fläche-zu-Umfang-Verhältnis
Zusammenfassung
Definition
Menge aller Punkte mit gleichem Abstand vom Mittelpunkt
Umfang
\[\displaystyle U = 2\pi r = \pi d\]
Fläche
\[\displaystyle A = \pi r^2\]
Durchmesser
\[\displaystyle d = 2r\]
|
|