Seitenhalbierende (Median)
Definition, Eigenschaften und Berechnung von Seitenhalbierenden in Dreiecken
Eine Seitenhalbierende (auch Median genannt) ist eine spezielle Linie in einem Dreieck, die einen Eckpunkt mit dem Mittelpunkt der gegenüberliegenden Seite verbindet. Sie ist eines der wichtigsten Konzepte in der Dreiecksgeometrie.
Seitenhalbierenden haben einzigartige Eigenschaften, insbesondere in Bezug auf den Schwerpunkt des Dreiecks, der ein fundamentales Konzept in der Mathematik und Physik ist.
Grundkonzept der Seitenhalbierenden
Die Seitenhalbierende eines Dreiecks ist ein Liniensegment, das einen Eckpunkt mit dem Mittelpunkt der gegenüberliegenden Seite verbindet.
Eine Seitenhalbierende (Median) eines Dreiecks ist eine Strecke, die:
- Von einem Eckpunkt des Dreiecks ausgeht
- Den Mittelpunkt der gegenüberliegenden Seite erreicht
- Das Dreieck in zwei Teile gleicher Fläche teilt
- Keine rechten Winkel: Im Gegensatz zu Höhen bilden Seitenhalbierenden keine rechten Winkel mit den Seiten
- Teilt in gleichflächige Dreiecke: Eine Seitenhalbierende teilt das Dreieck in zwei Dreiecke gleicher Fläche
- Drei pro Dreieck: Jedes Dreieck hat genau 3 Seitenhalbierenden (eine von jedem Eckpunkt)
- Schneiden sich im Schwerpunkt: Alle 3 Seitenhalbierenden schneiden sich in einem Punkt
Die drei Seitenhalbierenden eines Dreiecks
Jedes Dreieck hat genau drei Seitenhalbierenden, eine von jedem Eckpunkt zur Mittelpunkt der gegenüberliegenden Seite.
Anzahl
Jedes Dreieck hat genau 3 Seitenhalbierenden
Eine von jedem Eckpunkt
Schnittpunkt
Alle 3 schneiden sich in einem Punkt: dem Schwerpunkt
(Centroid)
Verhältnis
Der Schwerpunkt teilt jede Seitenhalbierende im Verhältnis 2:1
Von Eckpunkt zur Gegenseite
Der Punkt, in dem sich alle drei Seitenhalbierenden eines Dreiecks schneiden, wird Schwerpunkt oder Centroid genannt. Dieser Punkt:
- Liegt immer im Inneren des Dreiecks
- Teilt jede Seitenhalbierende im Verhältnis 2:1 (längerer Teil vom Eckpunkt)
- Ist das Gleichgewichtszentrum des Dreiecks (physikalischer Schwerpunkt)
- Hat eine besondere Bedeutung in Statik und Mechanik
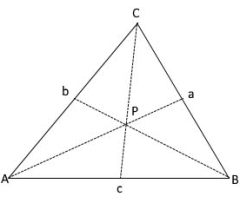
Die drei Seitenhalbierenden eines Dreiecks schneiden sich im Schwerpunkt P im Verhältnis 2:1
Das 2:1 Verhältnis des Schwerpunkts
Eine der wichtigsten Eigenschaften des Schwerpunkts ist, dass er jede Seitenhalbierende im Verhältnis 2:1 teilt.
Wenn die gesamte Seitenhalbierende die Länge 3x hat, dann ist:
• Entfernung vom Eckpunkt zum Schwerpunkt = 2x
• Entfernung vom Schwerpunkt zur Seitenmitte = x
Praktisches Beispiel
Berechnung der Seitenhalbierenden-Längen
Die Länge einer Seitenhalbierenden kann mit bekannten Seitenlängen des Dreiecks berechnet werden.
Formeln für Seitenhalbierenden
Für ein Dreieck mit den Seitenlängen a, b und c lauten die Formeln:
Seitenhalbierende zur Seite a (von Eckpunkt A):
Seitenhalbierende zur Seite b (von Eckpunkt B):
Seitenhalbierende zur Seite c (von Eckpunkt C):
Wobei a, b, c die Seitenlängen des Dreiecks sind und ma, mb, mc die Längen der entsprechenden Seitenhalbierenden.
Praktisches Beispiel: Berechnung der Seitenhalbierenden
Berechnung einer Seitenhalbierenden
Seitenhalbierenden vs. andere spezielle Linien
Dreiecke haben mehrere spezielle Linien. Die Seitenhalbierende unterscheidet sich von den anderen:
| Spezielle Linie | Definition | Schnittpunkt | Besonderheit |
|---|---|---|---|
| Seitenhalbierende | Eckpunkt zur Seitenmitte | Schwerpunkt | Teilt im Verhältnis 2:1 |
| Winkelhalbierende | Halbiert den Winkel | Inkreismittelpunkt | Gleichabstand zu Schenkeln |
| Höhe | Senkrecht zur Seite | Orthozentrum | Rechter Winkel zur Seite |
| Mittelsenkrechte | Senkrecht zur Seitenmitte | Umkreismittelpunkt | Zentrum des Umkreises |
Geometrische Eigenschaften der Seitenhalbierenden
Flächenteiling
Eine wichtige Eigenschaft der Seitenhalbierenden ist, dass sie das Dreieck in zwei Teile gleicher Fläche teilt.
Flächengleichheit
Eine Seitenhalbierende teilt das Dreieck in zwei Dreiecke mit gleicher Fläche.
Fläche₁ = Fläche₂
Schwerpunkt-Eigenschaft
Der Schwerpunkt ist der physikalische Gleichgewichtspunkt des Dreiecks.
Wenn man das Dreieck aufhängt, hängt es im Schwerpunkt im Gleichgewicht.
Zwei-zu-eins Teiling
Der Schwerpunkt teilt jede Seitenhalbierende im Verhältnis 2:1.
2 Teile vom Eckpunkt, 1 Teil zur Seitenmitte
Praktische Anwendungen der Seitenhalbierenden
- Physik und Mechanik: Bestimmung des Massenschwerpunkts von dreieckigen Objekten
- Ingenieurwesen: Berechnung von Tragwerken und Strukturen
- Architektur: Design von symmetrischen Strukturen und Bauwerken
- Computergrafik: Berechnung von Schwerpunkten für 3D-Modelle
- Geodäsie und Vermessung: Triangulierung und Landvermessung
- Navigation und Robotik: Berechnung von optimalen Routen durch dreieckige Regionen
Tipps und häufige Fehler
- Seitenmitte finden: Die Seitenhalbierende verbindet den Eckpunkt mit der Seitenmitte
- 2:1 Verhältnis merken: Der Schwerpunkt teilt immer im Verhältnis 2:1 von Eckpunkt zu Seitenmitte
- Mit Formeln berechnen: Für die Länge der Seitenhalbierenden nutzen Sie die bereitgestellten Formeln
- Alle 3 Seitenhalbierenden zeichnen: Sie schneiden sich immer im gleichen Punkt (Schwerpunkt)
- Gleichflächige Teile: Die Seitenhalbierende teilt das Dreieck immer in zwei gleich große Flächen
- FALSCH: Seitenhalbierende mit Winkelhalbierende verwechseln | RICHTIG: Seitenhalbierende geht zur Seitenmitte, nicht zur Winkelhalbierenden
- FALSCH: Schwerpunkt teilt Seitenhalbierende im Verhältnis 1:2 | RICHTIG: Das Verhältnis ist 2:1 vom Eckpunkt
- FALSCH: Schwerpunkt außerhalb des Dreiecks liegen | RICHTIG: Der Schwerpunkt liegt immer im Inneren des Dreiecks
- FALSCH: Seitenmitte falsch berechnen | RICHTIG: Die Seitenmitte ist der Mittelpunkt der Seite: (x₁+x₂)/2, (y₁+y₂)/2
Zusammenfassung der Seitenhalbierenden
Definition
Verbindung eines Eckpunkts mit der Mittelpunkt der gegenüberliegenden Seite
In Dreiecken
3 Seitenhalbierenden schneiden sich im Schwerpunkt im Verhältnis 2:1
Berechnung
\[m_a=\frac{ \sqrt{2b² + 2c² - a²}}{2}\] für alle drei Seitenhalbierenden
|
|