Theorem des Pythagoras

Der Satz des Pythagoras, spezielle rechtwinklige Dreiecke und Umkehrung

Der Satz des Pythagoras ist einer der wichtigsten Sätze der Geometrie. Er besagt, dass in einem rechtwinkligen Dreieck das Quadrat der Hypotenuse gleich der Summe der Quadrate der Katheten ist.

Die Hypotenuse ist die längste Seite und liegt immer dem rechten Winkel gegenüber.

Der Satz des Pythagoras

Grundformel:

Für ein rechtwinkliges Dreieck mit Katheten \(a\), \(b\) und Hypotenuse \(c\) gilt:

\[\displaystyle c^2 = a^2 + b^2\]

Die Länge der Hypotenuse ergibt sich aus:

\[\displaystyle c = \sqrt{a^2 + b^2}\]

Analog können die Katheten berechnet werden:

\[\displaystyle a = \sqrt{c^2 - b^2}, \quad b = \sqrt{c^2 - a^2}\]
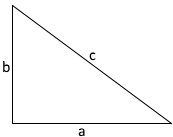
Pythagoras Dreieck

Rechtwinkliges Dreieck mit Katheten a, b und Hypotenuse c

Praktisches Beispiel

Berechnung der Hypotenuse
Gegeben: \(a = 3\), \(b = 4\)
Gesucht: \(c\)
Formel: \[\displaystyle c = \sqrt{a^2 + b^2}\]
Berechnung: \[\displaystyle c = \sqrt{3^2 + 4^2} = \sqrt{9 + 16} = \sqrt{25} = 5\]
Pythagoreische Tripel:

Ganzzahlige Lösungen wie (3, 4, 5) werden pythagoreische Tripel genannt. Weitere Beispiele: (5, 12, 13), (8, 15, 17), (7, 24, 25).

Spezielle rechtwinklige Dreiecke

30°-60°-90° Dreieck

Die Seitenlängen stehen in einem speziellen Verhältnis:

\[\displaystyle 1 : \sqrt{3} : 2\]

Wenn die Hypotenuse \(c\) bekannt ist, sind die Katheten:

\[\displaystyle a = \frac{c}{2}, \quad b = \frac{c}{2}\sqrt{3}\]
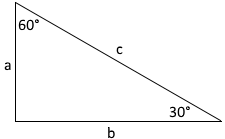
30-60-90 Dreieck

30°-60°-90° Dreieck mit Seitenverhältnis 1:√3:2

45°-45°-90° Dreieck

Dieses ist ein gleichschenkliges rechtwinkliges Dreieck mit gleichlangen Katheten:

\[\displaystyle a = b, \quad c = a\sqrt{2}\]

Oder umgekehrt:

\[\displaystyle a = \frac{c}{\sqrt{2}} = \frac{c\sqrt{2}}{2}\]
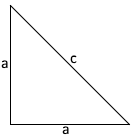
45-45-90 Dreieck

45°-45°-90° Dreieck mit Seitenverhältnis 1:1:√2

Umkehrung des Satzes des Pythagoras

Der Satz des Pythagoras lässt sich auch umkehren, um die Art des Dreiecks zu bestimmen:

Bestimmung des Dreieckstyps:

Für ein Dreieck mit den Seitenlängen \(a\), \(b\) und der längsten Seite \(c\) gilt:

\[\displaystyle c^2 < a^2 + b^2 \Rightarrow \text{Dreieck ist spitzwinklig}\]
\[\displaystyle c^2 = a^2 + b^2 \Rightarrow \text{Dreieck ist rechtwinklig}\]
\[\displaystyle c^2 > a^2 + b^2 \Rightarrow \text{Dreieck ist stumpfwinklig}\]

Zusammenfassung

Hauptsatz

In rechtwinkligen Dreiecken: \[\displaystyle c^2 = a^2 + b^2\]

30-60-90 Dreieck

Seitenverhältnis: \[\displaystyle 1 : \sqrt{3} : 2\]

45-45-90 Dreieck

Seitenverhältnis: \[\displaystyle 1 : 1 : \sqrt{2}\]



Winkelhalbierende
Seitenhalbierende
Höhe eines Dreiecks
Mittelsenkrechte eines Dreiecks
Satz des Pythagoras
Pythagoreisches-Tripel (3, 4, 5)
Kreis
Quadrat
Rechteck
Raute
Parallelogramm
Trapez








Ist diese Seite hilfreich?            
Vielen Dank für Ihr Feedback!

Das tut uns leid

Wie können wir die Seite verbessern?