Zinseszins berechnen
Die Kraft der Zinsen auf Zinsen - exponentielles Kapitalwachstum
Der Zinseszins ist eines der mächtigsten Konzepte in der Finanzwelt. Er beschreibt, wie Zinsen verdient werden - nicht nur auf das ursprüngliche Kapital, sondern auch auf die bereits verdienten Zinsen. Dies führt zu exponentiellem Wachstum über längere Zeiträume.
Der berühmte Albert Einstein soll gesagt haben: "Zinseszins ist die stärkste Kraft im Universum."
Das Konzept des Zinseszins
Beim Zinseszins werden die Zinsen jedem Jahr wieder zum Kapital hinzugefügt. Diese Zinsen erzeugen dann im nächsten Jahr wiederum neue Zinsen.
Einfache Zinsen vs. Zinseszinsen
Einfache Zinsen
Berechnung: Nur auf das Originalkapital
Jährlich gleich: Immer der gleiche Betrag
Berechnung: Z = K · p / 100
Beispiel: 1000€ zu 5% = 50€ pro Jahr
Zinseszinsen
Berechnung: Auf Kapital UND bisherige Zinsen
Jährlich wachsend: Immer mehr Zinsen
Berechnung: Kn = K₀(1+p/100)^n
Beispiel: 1000€ zu 5% = exponentielles Wachstum
Kapitalwachstum durch Zinseszins
Wenn Sie Geld für mehrere Jahre anlegen und die Zinsen dem Kapital aufgeschlagen werden, wächst das Kapital und damit auch der Zinsertrag pro Jahr bei gleichem Zinssatz.
Kn = K₀ · (1 + p/100)^n
wobei:
Kn = Kapital nach n Jahren
K₀ = Ausgangskapital
p = Jahreszinssatz (in Prozent)
n = Anzahl der Jahre
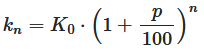
Beispiel: 1000 Euro über 5 Jahre
Sie legen 1000 Euro zu 5% Zinsen pro Jahr an und lassen die Zinsen am Konto. Wie viel haben Sie nach 5 Jahren?
| Jahr | Kapital Anfang | Zinsen (5%) | Kapital Ende |
|---|---|---|---|
| 1 | 1000,00 € | 50,00 € | 1050,00 € |
| 2 | 1050,00 € | 52,50 € | 1102,50 € |
| 3 | 1102,50 € | 55,13 € | 1157,63 € |
| 4 | 1157,63 € | 57,88 € | 1215,51 € |
| 5 | 1215,51 € | 60,78 € | 1276,28 € |
Weitere Beispiele
- 5000€ zu 3% für 10 Jahre: K₁₀ = 5000 · (1,03)^10 = 6720,31€
- 2000€ zu 4% für 20 Jahre: K₂₀ = 2000 · (1,04)^20 = 4760,44€
- 10000€ zu 2% für 30 Jahre: K₃₀ = 10000 · (1,02)^30 = 18113,88€
Kapital verdoppeln bei festem Zinssatz
Eine wichtige Frage: Wie lange dauert es, bis sich mein Geld verdoppelt? Dies wird berechnet, indem man Kn = 2·K₀ setzt.
n = ln(2) / ln(1 + p/100)
Diese Formel gibt die Anzahl der Jahre an, bis sich das Kapital verdoppelt.
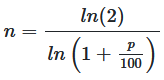
Beispiel: Verdoppelung bei 4% Zinsen
Wie lange dauert es, bis sich Ihr Kapital bei 4% Zinsen verdoppelt?
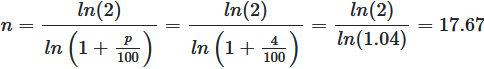
Die 70er-Regel (Faustformel)
Für schnelle Näherungswerte kann man die 70er-Regel verwenden:
n ≈ 70 / p
Diese Faustformel gibt einen schnellen Näherungswert ohne Taschenrechner.
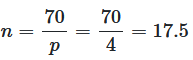
- 70er-Regel: n = 70 / p (für Zinssätze unter 5%)
- 72er-Regel: n = 72 / p (für Zinssätze über 5%, etwas genauer)
- 69,3er-Regel: n = 69,3 / p (mathematisch am genauesten)
Erforderlicher Zinssatz für Verdoppelung
Manchmal stellt sich die umgekehrte Frage: Welcher Zinssatz ist erforderlich, um das Kapital in einem bestimmten Zeitraum zu verdoppeln?
p = 100 · (ⁿ√2 - 1)
Diese Formel gibt den Zinssatz an, der nötig ist, um das Kapital in n Jahren zu verdoppeln.
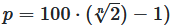
Beispiel: Verdoppelung in 10 Jahren
Welcher Zinssatz ist erforderlich, um das Kapital in 10 Jahren zu verdoppeln?
Weitere Beispiele
- Verdoppelung in 5 Jahren: p = 100 · (⁵√2 - 1) = 14,87% ≈ 14,9%
- Verdoppelung in 20 Jahren: p = 100 · (²⁰√2 - 1) = 3,53%
- Verdoppelung in 30 Jahren: p = 100 · (³⁰√2 - 1) = 2,34%
Verdopplungszeiten bei verschiedenen Zinssätzen
| Zinssatz | 70er-Regel (Näherung) | Genaue Formel | Differenz |
|---|---|---|---|
| 1% | 70,0 Jahre | 69,66 Jahre | 0,34 Jahre |
| 2% | 35,0 Jahre | 35,00 Jahre | 0,00 Jahre |
| 3% | 23,3 Jahre | 23,45 Jahre | -0,15 Jahre |
| 4% | 17,5 Jahre | 17,67 Jahre | -0,17 Jahre |
| 5% | 14,0 Jahre | 14,21 Jahre | -0,21 Jahre |
| 6% | 11,7 Jahre | 11,90 Jahre | -0,20 Jahre |
| 8% | 8,75 Jahre | 9,01 Jahre | -0,26 Jahre |
| 10% | 7,0 Jahre | 7,27 Jahre | -0,27 Jahre |
Praktische Anwendungen und Szenarien
Szenario 1: Altersversorgung planen
Ein 25-Jähriger legt 5000 Euro zu 5% an und möchte mit 65 Jahren in Rente gehen (40 Jahre):
Szenario 2: Kreditverschuldung
Ein Kredit von 10.000 Euro zu 6% verzinst sich jedes Jahr, wenn nicht bezahlt:
Szenario 3: Vergleich verschiedener Zinssätze
1000 Euro über 20 Jahre bei verschiedenen Zinssätzen:
- 2% Zinsen: 1000 · (1,02)^20 = 1485,95 Euro (Inflation ausgeglichen)
- 4% Zinsen: 1000 · (1,04)^20 = 2191,12 Euro (Gutes Wachstum)
- 6% Zinsen: 1000 · (1,06)^20 = 3206,16 Euro (Sehr gutes Wachstum)
Wichtige Erkenntnisse zum Zinseszins
- Exponentielles Wachstum: Das Kapital wächst nicht linear, sondern exponentiell
- Zeit ist kostbar: Je länger der Zeitraum, desto dramatischer der Effekt
- Auch kleine Unterschiede zählen: 1% mehr Zinsen kann über 30 Jahre 35% mehr Ertrag bringen
- Früh anfangen: 10 Jahre früher anfangen kann das Endergebnis verdoppeln
- Inflation: Ein Zinssatz von 2% bei 3% Inflation bedeutet Kaufkraftverlust!
- Gebühren: Bankgebühren können Gewinne aufzehren
- Regelmäßigkeit: Für maximales Wachstum sollten zusätzliche Einzahlungen erfolgen
- Liquidität: Geld im Zinseszins ist oft nicht sofort verfügbar
|
|