Winkel zwischen Vektoren

Formeln und Beispiele zur Berechnung des eingeschlossenen Winkels zwischen zwei Vektoren

Der Winkel zwischen zwei Vektoren ist eine wichtige Größe in der Vektorrechnung, die angibt, wie "ähnlich" die Richtungen zweier Vektoren sind. Ein Winkel von \(0°\) bedeutet, dass die Vektoren in die gleiche Richtung zeigen, während \(90°\) orthogonal (senkrecht) zueinander bedeutet, und \(180°\) bedeutet, dass sie in entgegengesetzte Richtungen zeigen.

Der Winkel zwischen zwei Vektoren wird berechnet, indem das Skalarprodukt und die Beträge der Vektoren verwendet werden. Diese Berechnung hat wichtige Anwendungen in Physik, Computergrafik und Ingenieurwesen.

Grundkonzept

Skalarprodukt

Inneres Produkt zweier Vektoren

Betrag

Länge eines Vektors

Kosinus

Trigonometrische Funktion

Arkuskosinus

Umkehrfunktion des Kosinus

Die Berechnung basiert auf:
  • Das Skalarprodukt \(\vec{a} \cdot \vec{b}\) misst die Ähnlichkeit der Richtungen
  • Der Betrag \(|\vec{a}|\) und \(|\vec{b}|\) normalisieren die Größen
  • Der Kosinus des Winkels gibt das Verhältnis an
  • Mit Arkuskosinus (arccos/acos) erhält man den Winkel in Grad oder Radiant

Formeln für den Winkel

Allgemeine Formel

Der Kosinus des Winkels \(\theta\) zwischen zwei Vektoren \(\vec{a}\) und \(\vec{b}\):

\[\displaystyle \cos(\theta) = \frac{\vec{a} \cdot \vec{b}}{|\vec{a}| \cdot |\vec{b}|}\]

Winkel in Radiant

Der Winkel in Radiant (zwischen 0 und \(\pi\)):

\[\displaystyle \theta = \arccos\left(\frac{\vec{a} \cdot \vec{b}}{|\vec{a}| \cdot |\vec{b}|}\right)\]

Umrechnung zu Grad

Der Winkel in Grad (zwischen 0° und 180°):

\[\displaystyle \theta_{\text{Grad}} = \arccos\left(\frac{\vec{a} \cdot \vec{b}}{|\vec{a}| \cdot |\vec{b}|}\right) \cdot \frac{180°}{\pi}\]

Ausführliche Formel für 2D-Vektoren

Für \(\vec{a} = \begin{bmatrix} a_1 \\ a_2 \end{bmatrix}\) und \(\vec{b} = \begin{bmatrix} b_1 \\ b_2 \end{bmatrix}\):

\[\displaystyle \cos(\theta) = \frac{a_1 b_1 + a_2 b_2}{\sqrt{a_1^2 + a_2^2} \cdot \sqrt{b_1^2 + b_2^2}}\]

Ausführliche Formel für 3D-Vektoren

Für \(\vec{a} = \begin{bmatrix} a_1 \\ a_2 \\ a_3 \end{bmatrix}\) und \(\vec{b} = \begin{bmatrix} b_1 \\ b_2 \\ b_3 \end{bmatrix}\):

\[\displaystyle \cos(\theta) = \frac{a_1 b_1 + a_2 b_2 + a_3 b_3}{\sqrt{a_1^2 + a_2^2 + a_3^2} \cdot \sqrt{b_1^2 + b_2^2 + b_3^2}}\]

Praktische Beispiele

Beispiel 1: Winkel zwischen 2D-Vektoren (45°)

Gegeben: \(\vec{x} = \begin{bmatrix} 3 \\ 0 \end{bmatrix}\) und \(\vec{y} = \begin{bmatrix} 5 \\ 5 \end{bmatrix}\)

Schritt 1: Skalarprodukt berechnen

\[\displaystyle \vec{x} \cdot \vec{y} = 3 \cdot 5 + 0 \cdot 5 = 15 + 0 = 15\]

Schritt 2: Beträge berechnen

\[\displaystyle |\vec{x}| = \sqrt{3^2 + 0^2} = \sqrt{9} = 3\]
\[\displaystyle |\vec{y}| = \sqrt{5^2 + 5^2} = \sqrt{50} = 5\sqrt{2} \approx 7.071\]

Schritt 3: Kosinus berechnen

\[\displaystyle \cos(\theta) = \frac{15}{3 \cdot 5\sqrt{2}} = \frac{15}{15\sqrt{2}} = \frac{1}{\sqrt{2}} = \frac{\sqrt{2}}{2} \approx 0.7071\]

Schritt 4: Winkel berechnen

\[\displaystyle \theta = \arccos\left(\frac{1}{\sqrt{2}}\right) = 45° = \frac{\pi}{4} \text{ rad}\]

Beispiel 2: Winkel zwischen orthogonalen 2D-Vektoren (90°)

Gegeben: \(\vec{u} = \begin{bmatrix} 1 \\ 0 \end{bmatrix}\) und \(\vec{v} = \begin{bmatrix} 0 \\ 1 \end{bmatrix}\)

\[\displaystyle \vec{u} \cdot \vec{v} = 1 \cdot 0 + 0 \cdot 1 = 0\]
\[\displaystyle \cos(\theta) = \frac{0}{1 \cdot 1} = 0\]
\[\displaystyle \theta = \arccos(0) = 90° = \frac{\pi}{2} \text{ rad}\]

Beispiel 3: Parallele Vektoren (0°)

Gegeben: \(\vec{a} = \begin{bmatrix} 2 \\ 2 \end{bmatrix}\) und \(\vec{b} = \begin{bmatrix} 4 \\ 4 \end{bmatrix}\)

\[\displaystyle \vec{a} \cdot \vec{b} = 2 \cdot 4 + 2 \cdot 4 = 8 + 8 = 16\]
\[\displaystyle |\vec{a}| = \sqrt{4 + 4} = 2\sqrt{2}, \quad |\vec{b}| = \sqrt{16 + 16} = 4\sqrt{2}\]
\[\displaystyle \cos(\theta) = \frac{16}{2\sqrt{2} \cdot 4\sqrt{2}} = \frac{16}{16} = 1\]
\[\displaystyle \theta = \arccos(1) = 0°\]

Beispiel 4: Entgegengesetzte Vektoren (180°)

Gegeben: \(\vec{p} = \begin{bmatrix} 3 \\ 0 \end{bmatrix}\) und \(\vec{q} = \begin{bmatrix} -3 \\ 0 \end{bmatrix}\)

\[\displaystyle \vec{p} \cdot \vec{q} = 3 \cdot (-3) + 0 \cdot 0 = -9\]
\[\displaystyle |\vec{p}| = 3, \quad |\vec{q}| = 3\]
\[\displaystyle \cos(\theta) = \frac{-9}{3 \cdot 3} = \frac{-9}{9} = -1\]
\[\displaystyle \theta = \arccos(-1) = 180° = \pi \text{ rad}\]

Grafische Darstellung

Die folgende Abbildung zeigt die grafische Darstellung des Winkels zwischen den Vektoren \(\vec{x} = \begin{bmatrix} 3 \\ 0 \end{bmatrix}\) und \(\vec{y} = \begin{bmatrix} 5 \\ 5 \end{bmatrix}\):

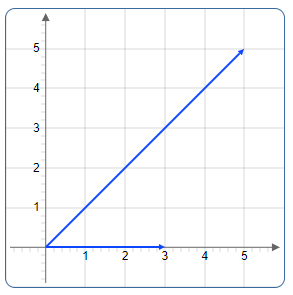
Winkel zwischen Vektoren

Winkel von 45° zwischen zwei Vektoren - dargestellt im Koordinatensystem

Spezialfälle und Interpretation

Interpretation des Winkels:
  • \(\theta = 0°\): Vektoren zeigen in gleiche Richtung (parallel), \(\cos(\theta) = 1\)
  • \(0° < \theta < 90°\): Spitzer Winkel, \(0 < \cos(\theta) < 1\), Vektoren ähnlich orientiert
  • \(\theta = 90°\): Vektoren sind orthogonal (senkrecht), \(\cos(\theta) = 0\), Skalarprodukt = 0
  • \(90° < \theta < 180°\): Stumpfer Winkel, \(-1 < \cos(\theta) < 0\), Vektoren verschiedene Richtungen
  • \(\theta = 180°\): Vektoren zeigen in entgegengesetzte Richtung, \(\cos(\theta) = -1\)

Verbindung zu anderen Konzepten

Die Berechnung des Winkels zwischen Vektoren hängt eng mit anderen Vektoroperationen zusammen:

  • Skalarprodukt: \(\vec{a} \cdot \vec{b} = |\vec{a}| |\vec{b}| \cos(\theta)\)
  • Betrag/Magnitude: Die Länge der Vektoren beeinflusst den Winkel nicht, nur die Richtung
  • Orthogonalität: Zwei Vektoren sind orthogonal, wenn ihr Skalarprodukt gleich Null ist
  • Normalisierung: Einheitsvektoren haben Betrag 1 und vereinfachen die Winkelberechnung

Weitere Informationen zum Skalarprodukt finden Sie hier, und zum Betrag eines Vektors hier.

Zusammenfassung

Allgemeine Formel

\[\displaystyle \cos(\theta) = \frac{\vec{a} \cdot \vec{b}}{|\vec{a}| \cdot |\vec{b}|}\]

Winkel (Radiant)

\[\displaystyle \theta = \arccos\left(\frac{\vec{a} \cdot \vec{b}}{|\vec{a}| \cdot |\vec{b}|}\right)\]

Winkel (Grad)

\[\displaystyle \theta° = \theta_{\text{rad}} \cdot \frac{180°}{\pi}\]

Orthogonal Test

\[\displaystyle \vec{a} \perp \vec{b} \iff \vec{a} \cdot \vec{b} = 0\]



Weitere Vektor Berechnungen

Vektor Definition
Vektor berechnen
Vektor Addition
Vektor Subtraktion
Vektor Betrag
Vektor Skalarprodukt
Vektor Kreuzprodukt
Winkel zwischen Vektoren
Vektor Spatprodukt















Ist diese Seite hilfreich?            
Vielen Dank für Ihr Feedback!

Das tut uns leid

Wie können wir die Seite verbessern?