Calculate angles from side lengths

Calculator and formula to compute triangle angles from side lengths a, b, c

Angle calculator

Law of Cosines calculation

This calculator computes the angles of a triangle from the side lengths a, b and c using the law of cosines.

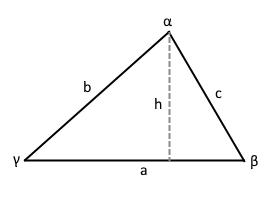
Enter triangle side lengths
Input: Enter the lengths of the 3 sides, then click 'Calculate'
Side a of the triangle
Side b of the triangle
Side c of the triangle
Calculated angles
Angle α:
Angle β:
Angle γ:
Angle sum in triangle: α + β + γ = 180°

Triangle with angles

Law of Cosines properties

Basis: Relationship between sides and angles in a triangle

3 sides → 3 angles α + β + γ = 180° cos α = (b²+c²-a²)/(2bc)

Triangle with side lengths a, b, c.
All angles are computable via the law of cosines.

Triangle


Angle calculation from side lengths: the law of cosines in action

The calculation of angles from side lengths uses the fundamental law of cosines:

  • Law of Cosines: c² = a² + b² - 2ab×cos(γ)
  • Rearranged: cos(γ) = (a² + b² - c²)/(2ab)
  • Angle: γ = arccos((a² + b² - c²)/(2ab))
  • All angles: α, β, γ computed analogously
  • Check: α + β + γ = 180°
  • Validity: Applicable to all triangle types

Geometric properties of angle calculation

The mathematical properties of computing angles from side lengths:

Law of Cosines application
  • Unique angle determination from 3 sides
  • Arccosine function for angle computation
  • Triangle inequality must hold
  • Valid for acute, right and obtuse triangles
Checks and validation
  • Angle sum α + β + γ = 180°
  • All angles between 0° and 180°
  • Triangle inequality: a+b > c, b+c > a, a+c > b
  • Cosine values between -1 and +1

Mathematics of angle calculation

The mathematical foundations of computing angles from side lengths:

Trigonometric relations
  • Law of Cosines: c² = a² + b² - 2ab cos(C)
  • Sine Law: a/sin(α) = b/sin(β) = c/sin(γ)
  • Arccosine for inverse angle computation
  • Conversion between degrees and radians
Algorithmic aspects
  • Numerical stability for extreme triangles
  • Rounding error control
  • Domain validation checks
  • Error handling for invalid inputs

Applications of angle calculation

Angle calculations from side lengths have many practical applications:

Surveying & Navigation
  • Triangulation and geodesy
  • GPS navigation and position fixing
  • Land surveying and cartography
  • Astronomical calculations
Engineering & Technology
  • Structural analysis and design
  • Mechanical engineering and gear design
  • Robotics and kinematics
  • Optics and ray tracing
Computer Graphics & Gaming
  • 3D modeling and animation
  • Collision detection in games
  • Lighting algorithms
  • Virtual reality and simulation
Education & Science
  • Geometry teaching and trigonometry
  • Physics: forces and vectors
  • Architecture and planning
  • Mathematical research

Formulas for angle calculation

Angle α
\[\alpha = \arccos\left(\frac{b^2+c^2-a^2}{2bc} \right)\]

Law of cosines rearranged for angle α

Angle β
\[\beta = \arccos\left(\frac{a^2+c^2-b^2}{2ac} \right)\]

Law of cosines rearranged for angle β

Angle γ
\[\gamma = \arccos\left(\frac{a^2+b^2-c^2}{2ab} \right)\]

Law of cosines rearranged for angle γ

General law of cosines
\[c^2 = a^2 + b^2 - 2ab \cos(\gamma)\]

Base form of the law of cosines

Angle sum
\[\alpha + \beta + \gamma = 180°\]

Check: sum of all angles in a triangle

Example for angle calculation

Given
Side a = 10 Side b = 7 Side c = 6

Find: all angles of the triangle

1. Compute angle α
\[\alpha = \arccos\left(\frac{7^2+6^2-10^2}{2 \cdot 7 \cdot 6}\right)\] \[\alpha = \arccos\left(\frac{49+36-100}{84}\right)\] \[\alpha = \arccos\left(\frac{-15}{84}\right) = 100.48°\]

Obtuse angle opposite the longest side

2. Compute angle β
\[\beta = \arccos\left(\frac{10^2+6^2-7^2}{2 \cdot 10 \cdot 6}\right)\] \[\beta = \arccos\left(\frac{100+36-49}{120}\right)\] \[\beta = \arccos\left(\frac{87}{120}\right) = 43.84°\]

Acute angle opposite the middle side

3. Compute angle γ
\[\gamma = \arccos\left(\frac{10^2+7^2-6^2}{2 \cdot 10 \cdot 7}\right)\] \[\gamma = \arccos\left(\frac{100+49-36}{140}\right)\] \[\gamma = \arccos\left(\frac{113}{140}\right) = 35.68°\]

Smallest angle opposite the shortest side

4. Angle sum check
α + β + γ = 100.48° + 43.84° + 35.68° = 180.00° ✓
Triangle type: obtuse triangle

The angle sum confirms the correctness of the calculation!

Law of Cosines: universal tool of trigonometry

The calculation of angles from side lengths using the law of cosines is a fundamental tool of trigonometry and analytic geometry. For centuries this elegant relationship has enabled precise computations in surveying, navigation, physics and engineering — from ancient land surveying to modern GPS systems.

The mathematical elegance of the law of cosines

The law of cosines unites geometry and trigonometry:

  • Universality: Valid for all triangle types — acute, right and obtuse
  • Completeness: From 3 side lengths all 3 angles can be uniquely determined
  • Generalization: Extends the Pythagorean theorem to arbitrary triangles
  • Symmetry: Each angle can be computed analogously by permuting sides
  • Consistency: Angle sum α + β + γ = 180° serves as a natural check
  • Numerical stability: Arccosine function is well-conditioned in typical cases

Historical development and significance

The history of angle computation mirrors the development of mathematics:

Ancient origins

Babylonian and Egyptian mathematicians already knew relations between sides and angles. Euclid's Elements formalized early trigonometrical concepts.

Islamic mathematics

Al-Biruni and other scholars developed systematic trigonometry; the law of cosines in modern form was articulated.

Renaissance and modern era

Mathematicians like François Viète refined trigonometrical methods. Calculus provided deeper insights.

Digital revolution

Computers and calculators made complex trigonometrical computations routine. GPS and navigation rely fundamentally on these principles.

Modern applications and technologies

Today angle calculation from side lengths is ubiquitous in technology:

  • Satellite navigation: GPS triangulation determines positions from distance measurements
  • Computer graphics: 3D rendering and animation rely on intensive trigonometrical computations
  • Robotics: Inverse kinematics for robot arm control
  • Structural analysis: Finite element methods in structural engineering
  • Optics: Ray tracing in camera and telescope systems
  • Geology: Seismic triangulation for earthquake localization

Numerical aspects and computer algebra

Practical implementation of angle computation presents interesting challenges:

Numerical stability

Extreme triangles (very sharp or nearly degenerate) can cause numerical instability. Special algorithms ensure accuracy.

Error handling

Violations of the triangle inequality or rounding errors require robust validation and error handling in implementations.

Optimization

Modern processors provide trigonometric instructions. Lookup tables and approximations speed up computations.

Precision

IEEE 754 floating-point arithmetic determines achievable accuracy. Symbolic math systems allow exact computations.

Future perspectives and developments

Angle computation remains relevant and continues to evolve:

  • Quantum computing: New algorithms for trigonometrical calculations on quantum hardware
  • Machine learning: Neural networks approximate complex trigonometrical functions
  • Augmented reality: Real-time angle calculations for immersive experiences
  • Autonomous vehicles: High-precision navigation and obstacle detection
  • Spaceflight: Interplanetary navigation and orbital mechanics
  • Nano-engineering: Molecular geometry and crystal structure analysis
Summary

Computing angles from side lengths using the law of cosines embodies the beauty and utility of mathematics. The elegant trigonometrical relation — α = arccos((b²+c²-a²)/(2bc)) — connects abstract geometric concepts with practical applications ranging from surveying to spaceflight. From ancient surveying to modern GPS systems, the law of cosines remains an indispensable tool of applied mathematics. Three sides, three angles, infinite possibilities.

Grad in Dezimal • Grad in Prozent • Winkelsumme von Vielecke • Winkel aus 3 Seiten • Ellipse • Kreis • Kreisbogen • Kreisring • Kreisring-Sektor • Kreissegment • Kreissektor • Kreiswinkel • Parabel • Quadratur des Kreises •