Winkel Grad in Prozent berechnen

Rechner und Formel zur Berechnung von Winkel Grad in Prozent

Winkel Grad Rechner

Steigungsmaß-Konvertierung

Mit diesem Rechner kann eine Winkelangabe von Grad in Prozent, oder umgekehrt berechnet werden. Der Prozentwert ist ein Maß für die Steigung.

Wichtiger Hinweis

Der Winkel in Grad muss größer als -90° und kleiner als 90° sein. 100% entspricht 45°, Werte über 100% sind möglich.

Was soll berechnet werden?
Grad° → Steigung%
Steigung% → Grad°
Bekannten Wert eingeben
Steigung: 100% bedeutet 45° Steigung (Höhe = Breite)
°
Winkel zwischen -90° und +90°
Konvertierungsergebnis
Steigung:
tan(45°) = 1.0 = 100% Steigung

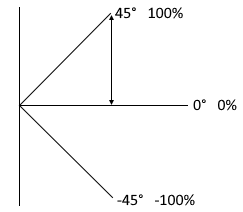
Steigungsdiagramm

Steigung Eigenschaften

Tangens-Beziehung: Steigung% = tan(Winkel°) × 100

0° = 0% 45° = 100% 90° = ∞%

Steigungsdiagramm: Winkel vs. Prozent
Höhe/Breite-Verhältnis als Prozentwert

Winkel in Prozent Diagramm

Steigungsmaß: Winkel und Prozent im praktischen Einsatz

Die Umrechnung zwischen Winkel und Steigungsprozent nutzt die Tangens-Funktion:

  • Steigungsprozent: Verhältnis Höhe zu horizontaler Strecke
  • 100% Steigung: 45° Winkel (Höhe = Breite)
  • Tangens-Beziehung: % = tan(Winkel) × 100
  • Gültigkeitsbereich: -90° < Winkel < +90°
  • Praktisch: Straßensteigungen, Dächer, Rampen
  • Umkehrung: Winkel = arctan(% / 100)

Geometrische Eigenschaften der Steigungsberechnung

Die mathematischen Eigenschaften der Winkel-Prozent-Umrechnung:

Tangens-Anwendung
  • Tangens als Steigungsmaß: tan(α) = Gegenkathete/Ankathete
  • Lineare Beziehung bei kleinen Winkeln
  • Asymptotisches Verhalten bei ±90°
  • Eindeutige Umkehrung durch Arcustangens
Steigungscharakteristik
  • 0° entspricht 0% (horizontal)
  • 45° entspricht 100% (45-Grad-Diagonale)
  • Steigungen über 100% möglich
  • Negative Steigungen für Gefälle

Mathematik der Steigungsberechnung

Die trigonometrischen Grundlagen der Winkel-Prozent-Umrechnung:

Trigonometrische Funktionen
  • Tangens: tan(α) = sin(α) / cos(α)
  • Arcustangens für Umkehrung: α = atan(tan(α))
  • Periodizität: tan(α + 180°) = tan(α)
  • Definitionslücken bei ±90°, ±270°, ...
Numerische Aspekte
  • Stabilität bei mittleren Winkeln (±45°)
  • Numerische Probleme nahe ±90°
  • Grad-Bogenmaß-Umrechnung erforderlich
  • Präzisionsverlust bei extremen Steigungen

Anwendungen der Steigungsberechnung

Steigungsberechnungen sind essentiell in vielen praktischen Bereichen:

Verkehr & Infrastruktur
  • Straßensteigungen und Gefälle
  • Eisenbahn-Trassenplanung
  • Rampen und Auffahrten
  • Brücken und Tunnel
Bauwesen & Architektur
  • Dachneigungen und Entwässerung
  • Barrierefreie Zugänge
  • Treppen und Handläufe
  • Geländemodellierung
Vermessung & Geologie
  • Topographische Karten
  • Hangstabilitätsanalyse
  • Erosionsberechnungen
  • Geodätische Messungen
Technik & Maschinenbau
  • Förderbänder und Rutschten
  • Hydraulische Systeme
  • Keilverbindungen
  • Schrägaufzüge

Formeln: Grad / Prozent Umrechnung

Winkel Grad → Prozent
\[\text{Prozent} = \tan(\text{Grad}) \times 100\]

Tangens-Funktion für Steigungsberechnung

Winkel Prozent → Grad
\[\text{Grad} = \arctan\left(\frac{\text{Prozent}}{100}\right)\]

Arcustangens für Winkelberechnung

Tangens-Definition
\[\tan(\alpha) = \frac{\text{Gegenkathete}}{\text{Ankathete}} = \frac{\text{Höhe}}{\text{Breite}}\]

Grunddefinition der Tangens-Funktion

Gültigkeitsbereich
\[-90° < \alpha < +90°\]

Definitionsbereich für praktische Anwendungen

Rechenbeispiele für Steigungsberechnungen

Beispiel 1: Grad → Prozent
30° Steigung
\[\text{Prozent} = \tan(30°) \times 100\] \[= 0.5774 \times 100\] \[= 57.74\%\]

30° entspricht etwa 58% Steigung

Beispiel 2: Prozent → Grad
25% Steigung
\[\text{Grad} = \arctan\left(\frac{25}{100}\right)\] \[= \arctan(0.25)\] \[= 14.04°\]

25% entspricht etwa 14° Neigung

Praktische Referenzwerte
0° = 0%
Horizontal
26.57° = 50%
Steile Straße
45° = 100%
45° Diagonale
63.43° = 200%
Sehr steil

Häufige Steigungswinkel in der Praxis

Steigungsmaß: Brücke zwischen Winkel und Praxis

Die Umrechnung zwischen Winkel und Steigungsprozent verbindet abstrakte trigonometrische Konzepte mit praktischen Anwendungen im Bauwesen, Verkehr und der Technik. Die Tangens-Funktion - mathematisch elegant, praktisch unverzichtbar - ermöglicht es, Neigungen intuitiv als Prozentsatz zu verstehen und präzise zu berechnen.

Die intuitive Bedeutung des Steigungsmaßes

Das Steigungsprozent macht Winkel greifbar und praktisch nutzbar:

  • Anschaulichkeit: 100% bedeutet "pro Meter horizontal steigt es einen Meter"
  • Praktische Relevanz: Verkehrsschilder, Bauvorschriften, Normen verwenden Prozent
  • Tangens-Eleganz: tan(α) = Steigung als natürliche trigonometrische Beziehung
  • Unbegrenztheit: Steigungen über 100% möglich (im Gegensatz zu Sinus/Cosinus)
  • Linearität: Bei kleinen Winkeln näherungsweise linear
  • Vorzeichenlogik: Negative Werte für Gefälle, positive für Steigung
Zusammenfassung

Die Steigungsberechnung mittels Tangens-Funktion - Prozent = tan(Grad) × 100 - ist ein perfektes Beispiel für angewandte Trigonometrie. Sie übersetzt abstrakte Winkelmaße in greifbare Prozentsätze, die jeder versteht: 45° wird zu verständlichen 100% Steigung. Von der Straßenplanung über Dachkonstruktionen bis zur Geländemodellierung bleibt diese Umrechnung ein unverzichtbares Werkzeug. Sie zeigt, wie Mathematik praktische Probleme elegant löst und komplexe Sachverhalte in intuitive Maße übersetzt.

Grad in Dezimal • Grad in Prozent • Winkelsumme von Vielecke • Winkel aus 3 Seiten • Ellipse • Kreis • Kreisbogen • Kreisring • Kreisring-Sektor • Kreissegment • Kreissektor • Kreiswinkel • Parabel • Quadratur des Kreises •