Winkel aus Seitenlängen berechnen
Rechner und Formel zur Berechnung der Winkel zu den Seitenlängen a,b,c
Winkel Rechner
Kosinussatz-Berechnung
Mit diesem Rechner werden die Winkel eines Dreiecks aus den Seitenlängen a, b und c mittels Kosinussatz berechnet.
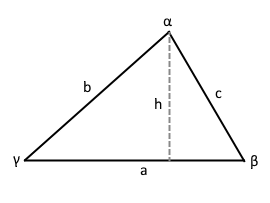
Dreieck mit Winkeln
Kosinussatz Eigenschaften
Grundlage: Beziehung zwischen Seiten und Winkeln im Dreieck
Dreieck mit Seitenlängen a, b, c.
Alle Winkel berechenbar durch Kosinussatz.
|
|
Winkelberechnung aus Seitenlängen: Der Kosinussatz in Aktion
Die Berechnung der Winkel aus Seitenlängen nutzt den fundamentalen Kosinussatz:
- Kosinussatz: c² = a² + b² - 2ab×cos(γ)
- Umstellung: cos(γ) = (a² + b² - c²)/(2ab)
- Winkel: γ = arccos((a² + b² - c²)/(2ab))
- Alle Winkel: α, β, γ analog berechenbar
- Kontrolle: α + β + γ = 180°
- Gültigkeit: Für alle Dreiecksarten
Geometrische Eigenschaften der Winkelberechnung
Die mathematischen Eigenschaften der Winkelberechnung aus Seitenlängen:
Kosinussatz-Anwendung
- Eindeutige Winkelbestimmung aus 3 Seiten
- Arcuscosinus-Funktion für Winkelberechnung
- Dreiecksungleichung muss erfüllt sein
- Gültig für spitze, rechte und stumpfe Winkel
Kontrollen und Validierung
- Winkelsumme α + β + γ = 180°
- Alle Winkel zwischen 0° und 180°
- Dreiecksungleichung: a+b > c, b+c > a, a+c > b
- Cosinus-Werte zwischen -1 und +1
Mathematik der Winkelberechnung
Die mathematischen Grundlagen der Winkelberechnung aus Seitenlängen:
Trigonometrische Beziehungen
- Kosinussatz: c² = a² + b² - 2ab cos(C)
- Sinussatz: a/sin(α) = b/sin(β) = c/sin(γ)
- Arcuscosinus für Winkelumkehrung
- Gradmaß und Bogenmaß-Umrechnung
Algorithmische Aspekte
- Numerische Stabilität bei extremen Dreiecken
- Rundungsfehler-Kontrolle
- Definitionsbereich-Überprüfung
- Fehlerbehandlung bei ungültigen Eingaben
Anwendungen der Winkelberechnung
Winkelberechnungen aus Seitenlängen haben vielfältige praktische Anwendungen:
Vermessung & Navigation
- Triangulation und Geodäsie
- GPS-Navigation und Positionsbestimmung
- Landvermessung und Kartographie
- Astronomische Berechnungen
Ingenieurswesen & Technik
- Statik und Konstruktionsberechnung
- Maschinenbau und Getriebe-Design
- Robotik und Kinematik
- Optik und Strahlengang-Berechnung
Computer Graphics & Gaming
- 3D-Modellierung und Animation
- Collision Detection in Spielen
- Beleuchtungs-Algorithmen
- Virtuelle Realität und Simulation
Bildung & Wissenschaft
- Geometrie-Unterricht und Trigonometrie
- Physik: Kräfte und Vektoren
- Architektur und Bauplanung
- Mathematische Forschung
Formeln zur Berechnung der Winkel
Winkel α
Kosinussatz umgestellt nach Winkel α
Winkel β
Kosinussatz umgestellt nach Winkel β
Winkel γ
Kosinussatz umgestellt nach Winkel γ
Kosinussatz Allgemein
Grundform des Kosinussatzes
Winkelsumme
Kontrolle: Summe aller Winkel im Dreieck
Rechenbeispiel für Winkelberechnung
Gegeben
Gesucht: Alle Winkel des Dreiecks
1. Winkel α berechnen
Stumpfer Winkel gegenüber der längsten Seite
2. Winkel β berechnen
Spitzer Winkel gegenüber mittlerer Seite
3. Winkel γ berechnen
Kleinster Winkel gegenüber kürzester Seite
4. Kontrolle der Winkelsumme
Die Winkelsumme bestätigt die Korrektheit der Berechnung!
Der Kosinussatz: Universalwerkzeug der Trigonometrie
Die Berechnung von Winkeln aus Seitenlängen mittels Kosinussatz gehört zu den fundamentalen Werkzeugen der Trigonometrie und analytischen Geometrie. Seit Jahrhunderten ermöglicht diese elegante mathematische Beziehung präzise Berechnungen in Vermessung, Navigation, Physik und Ingenieurswesen - von der antiken Landvermessung bis zu modernen GPS-Systemen.
Die mathematische Eleganz des Kosinussatzes
Der Kosinussatz vereint Geometrie und Trigonometrie in perfekter Harmonie:
- Universalität: Gültig für alle Dreiecksarten - spitz-, recht- und stumpfwinklig
- Vollständigkeit: Aus 3 Seitenlängen alle 3 Winkel eindeutig bestimmbar
- Verallgemeinerung: Erweitert den Satz des Pythagoras auf beliebige Dreiecke
- Symmetrie: Jeder Winkel analog berechenbar durch Vertauschung der Seiten
- Konsistenz: Winkelsumme α + β + γ = 180° als natürliche Kontrolle
- Numerische Stabilität: Arcuscosinus-Funktion gut konditioniert
Historische Entwicklung und Bedeutung
Die Geschichte der Winkelberechnung spiegelt die Entwicklung der Mathematik wider:
Antike Ursprünge
Bereits babylonische und ägyptische Mathematiker kannten Beziehungen zwischen Seiten und Winkeln. Euklids "Elemente" formalisierte erste trigonometrische Konzepte.
Islamische Mathematik
Al-Biruni und andere islamische Gelehrte entwickelten systematische Trigonometrie. Der Kosinussatz in heutiger Form wurde explizit formuliert.
Renaissance und Moderne
François Viète und andere Renaissance-Mathematiker perfektionierten trigonometrische Methoden. Die Infinitesimalrechnung ermöglichte tiefere Einsichten.
Digitale Revolution
Computer und Taschenrechner machten komplexe trigonometrische Berechnungen alltäglich. GPS und Navigation basieren fundamental auf diesen Prinzipien.
Moderne Anwendungen und Technologien
Heute ist die Winkelberechnung aus Seitenlängen allgegenwärtig in der Technik:
- Satellitennavigation: GPS-Triangulation bestimmt Positionen über Entfernungsmessungen
- Computer Graphics: 3D-Rendering und Animation nutzen intensive trigonometrische Berechnungen
- Robotik: Inverse Kinematik für Roboterarm-Steuerung
- Strukturanalyse: Finite-Elemente-Methoden in der Baustatik
- Optik: Strahlenverfolgung in Kamera- und Teleskopsystemen
- Geologie: Seismische Triangulation für Erdbebenortung
Numerische Aspekte und Computeralgebra
Die praktische Umsetzung der Winkelberechnung bringt interessante Herausforderungen:
Numerische Stabilität
Extreme Dreiecke (sehr spitz oder fast entartet) können zu numerischen Instabilitäten führen. Spezielle Algorithmen gewährleisten Genauigkeit.
Fehlerbehandlung
Verletzung der Dreiecksungleichung oder Rundungsfehler erfordern robuste Validierung und Fehlerbehandlung in Implementierungen.
Optimierung
Moderne Prozessoren bieten spezielle trigonometrische Instruktionen. Lookup-Tabellen und Approximationen beschleunigen Berechnungen.
Präzision
IEEE 754 Gleitkomma-Arithmetik bestimmt erreichbare Genauigkeit. Symbolische Mathematiksysteme ermöglichen exakte Berechnungen.
Zukunftsperspektiven und Entwicklungen
Die Winkelberechnung bleibt auch in Zukunft relevant und entwickelt sich weiter:
- Quantencomputing: Neue Algorithmen für trigonometrische Berechnungen auf Quantencomputern
- Machine Learning: Neuronale Netze approximieren komplexe trigonometrische Funktionen
- Augmented Reality: Echtzeitwinkelberechnungen für immersive Erfahrungen
- Autonome Fahrzeuge: Hochpräzise Navigation und Hinderniserkennung
- Raumfahrt: Interplanetare Navigation und Orbitmechanik
- Nano-Engineering: Molekulare Geometrie und Kristallstrukturanalyse
Zusammenfassung
Die Berechnung von Winkeln aus Seitenlängen mittels Kosinussatz verkörpert die Schönheit und Nützlichkeit der Mathematik. Diese elegante trigonometrische Beziehung - α = arccos((b²+c²-a²)/(2bc)) - verbindet abstrakte geometrische Konzepte mit praktischen Anwendungen von der Landvermessung bis zur Raumfahrt. Von antiken Vermessungsarbeiten bis zu modernen GPS-Systemen bleibt der Kosinussatz ein unverzichtbares Werkzeug der angewandten Mathematik. Er erinnert uns daran, dass in der scheinbaren Einfachheit einer geometrischen Beziehung die Grundlage für unzählige technologische Errungenschaften liegt - drei Seiten, drei Winkel, unendliche Möglichkeiten.