Circular Segment Calculator

Calculator and formulas for circular segment calculations (circular cap)

Circular Segment Calculator

The Circular Segment

A circular segment is a circular cap that is separated from the circle by a straight chord. Also called a "circular cap" or "circular segment".

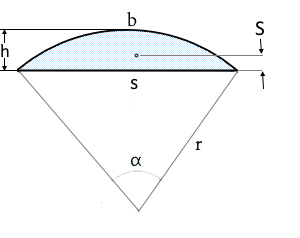
Enter Circular Segment Parameters
Select the calculation mode
Radius of the circle
Which property is known?
Value of the selected property
Height of the segment
Which property is known?
Value of the selected property
Circular Segment Properties

Chord boundary: Cut off by a straight chord

Radius r Height h Chord s Arc b
Circular Segment Calculation Results
Angle α:
Height h:
Area A:
Perimeter P:
Arc length b:
Chord s:
Centroid S:
Radius r:

Circular Segment Structure

A circular segment is the smaller area of a split circle.
Separated from the remaining circle by a straight chord.

Circular Segment

What is a Circular Segment?

A circular segment is a fundamental geometric shape with special properties:

  • Definition: Circular cap separated by a chord
  • Two boundaries: Arc and straight chord
  • Asymmetric shape: Different from circular sector
  • Height h: Distance from the chord to the farthest arc point
  • Versatile size: From shallow cap to almost semicircle
  • Practical relevance: Architecture, optics, mechanical engineering

Geometric Properties of the Circular Segment

The circular segment has characteristic geometric properties:

Basic Parameters
  • Radius r: Radius of the original circle
  • Height h: Distance from chord to farthest arc point
  • Chord s: Straight boundary line of the segment
  • Central angle α: Angle of the associated circular sector
Special Properties
  • Asymmetry: Different from radially symmetric sectors
  • Height relation: h = r - r·cos(α/2)
  • Centroid: Lies on the symmetry axis
  • Limit case: For h=r it becomes a semicircle

Mathematical Relationships

The circular segment follows complex mathematical laws:

Area Calculation
A = ½ r² (α - sin α)

Segment = sector minus triangle. Complex relation between angle and area.

Height-Radius Relation
h = r (1 - cos(α/2))

The height depends trigonometrically on the half central angle.

Applications of Circular Segments

Circular segments have a wide range of practical applications:

Architecture & Construction
  • Dome segments and vault sections
  • Bridge arches and tunnel profiles
  • Window shapes and archways
  • Roof constructions and coverings
Mechanical Engineering & Technology
  • Cams and curve controls
  • Containers and tank cross-sections
  • Valves and flaps
  • Rotors and turbine profiles
Optics & Lighting
  • Lenses and optical elements
  • Reflectors and mirrors
  • Prisms and light guides
  • Lighting optics
Hydraulics & Water Engineering
  • Channel cross-sections and pipes
  • Weirs and overflow edges
  • Locks and hydraulic structures
  • Flow optimization

Formulas for the Circular Segment

Area A
\[A = \frac{r^2}{2}(\alpha - \sin \alpha)\]

Circular sector minus inscribed triangle

Height h
\[h = r\left(1 - \cos\left(\frac{\alpha}{2}\right)\right)\]

Distance from chord to farthest arc point

Chord s
\[s = 2r \sin\left(\frac{\alpha}{2}\right)\]

Straight boundary line of the segment

Arc length b
\[b = r \alpha\]

Curved boundary (angle in radians)

Perimeter P
\[P = s + b = 2r \sin\left(\frac{\alpha}{2}\right) + r\alpha\]

Chord plus arc

Central Angle α (from height)
\[\alpha = 2 \arccos\left(1 - \frac{h}{r}\right)\]

Recompute the angle from height and radius

Centroid S
\[S = \frac{s^3}{12A} - r\cos\left(\frac{\alpha}{2}\right)\]

Distance of the centroid from the circle center

Height h (from chord)
\[h = r - \sqrt{r^2 - \frac{s^2}{4}}\]

Compute height when chord is known

Calculation Example for a Circular Segment

Given
Radius r = 20 Height h = 5

Find: All properties of the circular segment

1. Compute Central Angle
\[\alpha = 2 \arccos\left(1 - \frac{5}{20}\right)\] \[\alpha = 2 \arccos(0.75) = 82.82°\]

Convert height and radius to angle

2. Compute Chord
\[s = 2 \times 20 \times \sin(41.41°)\] \[s = 40 \times 0.663 = 26.51\]

Chord via trigonometric relation

3. Area and Arc Length
\[A = \frac{20^2}{2}(1.446 - \sin(82.82°)) = 73.42\] \[b = 20 \times 1.446 = 28.92\]

Area and arc length of the segment

4. Perimeter and Centroid
\[P = 26.51 + 28.92 = 55.43\] \[S = \frac{26.51^3}{12 \times 73.42} - 20 \cos(41.41°) = 1.52\]

Total perimeter and centroid distance

5. Complete Circular Segment
Radius r = 20.00 Height h = 5.00 Central Angle α = 82.82° Chord s = 26.51
Area A = 73.42 Arc length b = 28.92 Perimeter P = 55.43 Centroid S = 1.52

A circular segment with medium height - typical for architectural applications

The Circular Segment: Asymmetric Circle Geometry

The circular segment is one of the most fascinating shapes of circle geometry. Unlike the radially symmetric circular sector, the segment is bounded by a chord, which leads to asymmetric but still elegant mathematical relations. This shape is widely used in architecture, engineering and optics.

Definition and Structural Features

The circular segment differs fundamentally from other circle shapes:

  • Chord boundary: A straight line separates the segment from the rest of the circle
  • Asymmetric structure: No radial symmetry as with the circular sector
  • Height parameter: The height h is a characteristic measure of the segment shape
  • Two boundaries: Arc and straight chord form the perimeter
  • Variability: From shallow cap to nearly semicircular segments

Mathematical Complexity and Elegance

The mathematics of the circular segment combines various geometric concepts:

Difference principle

The segment area is the difference between sector and inscribed triangle: A = ½ r² (α - sin α). This elegantly simple formula hides complex trigonometric relations.

Height trigonometry

The relation h = r(1 - cos(α/2)) connects the intuitive height with the abstract central angle via trigonometric functions.

Centroid calculation

The centroid requires integration over the asymmetric shape: S = s³/(12A) - r·cos(α/2). This formula shows the mathematical sophistication of segment geometry.

Parameter conversion

Converting between height, chord, angle and radius requires inverse trigonometric functions, which makes the segment mathematically more demanding than other circle shapes.

Architectural and Engineering Significance

Circular segments are fundamental in practical application:

Structural advantage

Segment-shaped arches and vaults use the natural compression distribution of circular structures, while the flat chord offers practical advantages for support constructions.

Material optimization

The segment shape enables optimal material-performance ratios: maximum structural efficiency with minimal material for roofs and vaults.

Hydraulic applications

In water engineering, segment-shaped channel cross-sections enable optimal flow properties at different fill levels - a classic optimization problem in hydraulics.

Optical systems

Lens segments and aspherical optics use the controlled curvature of circular segments for precise light guidance and aberration correction.

Special Cases and Optimization Problems

The circular segment leads to interesting optimization problems:

  • Tank fill level: Calculation of volumes in partially filled cylindrical tanks
  • Bridge construction: Optimal arch height for maximum load capacity at given span
  • Solar technology: Parabolic mirror segments for optimal light concentration
  • Flow engineering: Channel profiles for minimal flow resistance
  • Architecture: Window shapes for optimal light yield under structural constraints

Calculation Strategies and Numerical Aspects

Practical calculation of circular segments requires different approaches:

Direct formulas

When radius and angle are known, direct trigonometric formulas lead to exact results. This is the most mathematically elegant way.

Iterative methods

When height and chord are given, inverse trigonometric functions must be computed numerically - a typical engineering math problem.

Approximation formulas

For shallow segments (h << r) there are approximation formulas that simplify practical calculations without significant loss of accuracy.

CAD integration

Modern CAD systems use parametric representations of circular segments that allow automatic recalculation when parameters change.

Summary

The circular segment embodies the perfect balance between mathematical complexity and practical applicability. Its asymmetric structure - bounded by arc and chord - leads to elegant but demanding mathematical relations that require inverse trigonometric functions and difference computations. From ancient architecture to modern engineering, the circular segment remains a fundamental shape for structural, hydraulic and optical applications. Its mathematical sophistication - exemplified by the centroid formula or the height-angle relation - makes it an ideal object for understanding advanced geometric concepts. In a world where optimization and material efficiency become ever more important, the circular segment remains an indispensable tool for engineers, architects and mathematicians.

Angle functions

From Deg, Min, Sec to Decimal • From Degree to Percent • Angle sum • Side lengths from angles

Circular functions

Annulus • Annulus sector • Circle • Circular angles • Circular arcs • Circular sector • Circular segment • Ellipse • Parabolic arch • Squaring the Circle