Circular Angles Calculator

Calculator and formulas for circular angle calculations

Circular Angles Calculator

Circular Angles

Circular angles are the characteristic angles in circle geometry: central angle μ, tangent angle θ and their relationships.

Enter Circular Angle Parameters
Select the first known parameter
Value of the first parameter
Select the second known parameter
Value of the second parameter
Circular Angle Properties

Angle relationships: θ = μ/2 (tangent angle = half the central angle)

Central Angle μ Tangent Angle θ Radius r Chord s
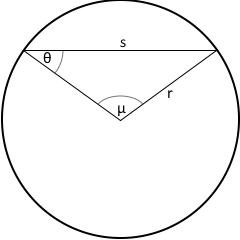
Circular Angles Calculation Results
Tangent Angle θ:
Central Angle μ:
Radius r:
Chord s:

Circular Angles Structure

Circular angles demonstrate fundamental angular relationships.
θ = μ/2 is one of the most important relationships in circle geometry.

Circular Angles

What are Circular Angles?

Circular angles are fundamental angles in circle geometry:

  • Central angle μ: Angle at the circle center
  • Tangent angle θ: Angle between radius and chord
  • Basic relation: θ = μ/2
  • Geometric basis: Used in many circle calculations
  • Trigonometric connection: Links to sine and cosine
  • Practical relevance: Navigation, surveying, optics

Geometric Properties of Circular Angles

Circular angles follow basic geometric laws:

Angle Types
  • Central angle μ: Measured from the center
  • Tangent angle θ: Between radius and chord
  • Inscribed angle: Measured from the circumference
  • Interior angles: In the triangle center-chord endpoints
Fundamental Relations
  • Half-angle rule: θ = μ/2
  • Trigonometric link: sin(θ) = s/(2r)
  • Law of cosines application: Chord calculation
  • Symmetry: Isosceles triangles

Mathematical Relationships

Circular angles form the basis of many trigonometric relationships:

Half-angle Theorem
θ = μ/2

The tangent angle is always half the central angle. Fundamental law of circle geometry.

Chord Relationship
s = 2r·sin(θ)

Compute the chord from tangent angle and radius. Direct trigonometric link.

Applications of Circular Angle Calculations

Circular angles are essential in many fields:

Navigation & Surveying
  • GPS calculations and triangulation
  • Compass navigation and bearings
  • Land surveying and cartography
  • Astronomical positioning
Mechanical & Engineering
  • Gear geometry and tooth profiles
  • Cam discs and linkages
  • Robot kinematics and joint angles
  • Precision mechanics and horology
Optics & Photonics
  • Lens systems and aberrations
  • Reflecting telescopes and mirrors
  • Laser beams and ray paths
  • Camera optics and image quality
Architecture & Construction
  • Domes and vault constructions
  • Bridge arches and structural designs
  • Sun studies and shadowing
  • Circular buildings and spiral staircases

Formulas for Circular Angles

Tangent Angle θ
\[\theta = \frac{\mu}{2}\]

Fundamental half-angle relation

Central Angle μ
\[\mu = \arccos\left(\frac{2r^2 - s^2}{2r^2}\right)\]

Compute from radius and chord

Chord s
\[s = \sqrt{2r^2(1 - \cos(\mu))}\]

Compute from radius and central angle

Radius r
\[r = \sqrt{\frac{s^2}{2(1 - \cos(\mu))}}\]

Compute from chord and central angle

Alternative Chord Formula
\[s = 2r \sin(\theta) = 2r \sin\left(\frac{\mu}{2}\right)\]

Via tangent angle or half central angle

Inscribed Angle Relation
\[\text{Inscribed angle} = \frac{\mu}{2} = \theta\]

Inscribed angle = tangent angle (Thales' circle)

Calculation Example for Circular Angles

Given
Radius r = 25 Chord s = 30

Find: Central angle μ and tangent angle θ

1. Compute Central Angle
\[\mu = \arccos\left(\frac{2 \times 25^2 - 30^2}{2 \times 25^2}\right)\] \[\mu = \arccos\left(\frac{1250 - 900}{1250}\right) = \arccos(0.28)\] \[\mu = 73.74°\]

Application of the law of cosines

2. Compute Tangent Angle
\[\theta = \frac{\mu}{2} = \frac{73.74°}{2} = 36.87°\]

Fundamental half-angle relation

3. Verification via Sine
\[s = 2r \sin(\theta) = 2 \times 25 \times \sin(36.87°)\] \[s = 50 \times 0.6 = 30.00\] ✓

Confirmation via alternative computation

4. Geometric Interpretation
3-4-5 triangle similarity
\[\frac{s}{2r} = \frac{30}{50} = 0.6 = \sin(36.87°)\]

Connection to known triangle ratios

5. Complete Circular Angle Solution
Radius r = 25.00 Chord s = 30.00 Central Angle μ = 73.74°
Tangent Angle θ = 36.87° sin(θ) = 0.6 cos(θ) = 0.8

A classic 3-4-5 triangle ratio in circular angle representation

Circular Angles: Fundamental Geometry and Trigonometry

Circular angles form the core of circle geometry and are essential for understanding trigonometric relationships. The elegant relation θ = μ/2 between tangent and central angles is one of the most useful geometrical rules.

Historical development and mathematical significance

The theory of circular angles has a rich mathematical history:

  • Ancient foundations: Thales and Euclid already recognized fundamental angle relations
  • Medieval development: Islamic mathematicians refined trigonometric applications
  • Renaissance advances: Precise angle measurements for navigation and astronomy
  • Modern applications: From GPS systems to robot control
  • Theoretical basis: Foundation for complex numbers and Fourier analysis

Fundamental angular relations

Circular angle theory is based on elegant mathematical principles:

Half-angle theorem

The relation θ = μ/2 is not only a practical formula but an expression of the circle's fundamental symmetry. It elegantly connects central and peripheral angle measures.

Trigonometric connection

Circular angles form the geometric basis for sine, cosine and tangent. The unit-circle definition of trigonometric functions is directly based on circular angles.

Inscribed angle theorem

All inscribed angles subtending the same arc are equal - a fundamental theorem following from circular angle theory with countless applications.

Complex numbers

In the complex plane, circular angles correspond to rotations, making them fundamental for Fourier transforms and signal processing.

Practical applications in science and engineering

Circular angles are essential in numerous technical fields:

Navigation and GPS

GPS calculations are based on spherical trigonometry, developed from circular angle principles. Satellite positioning continuously uses angle computations.

Robotics and automation

Robot joints and motion control use circular angles for precise positioning and path planning. Inverse kinematics is impossible without angle calculations.

Optics and laser technology

Lens systems, ray paths and aberration correction use circular angle calculations for precise optical designs. Every camera and telescope is built on these principles.

Mechanical design

Gear geometry, cam profiles and precision mechanics require exact angle calculations. Modern mechanical engineering would not be possible without circular angle theory.

Calculation strategies and numerical aspects

Practical computation of circular angles requires different approaches:

  • Direct formulas: When base parameters are known, trigonometric formulas give exact results
  • Inverse trigonometry: arcsin, arccos, arctan for reverse calculations - numerically demanding
  • Iterative methods: For complex systems with multiple unknowns
  • CAD integration: Automatic angle calculation in modern CAD tools
  • Precision requirements: Astronomy and GPS require micro-arcsecond accuracy

Advanced mathematical connections

Circular angles connect different mathematical fields:

Analytic geometry

Circle equations and parametric representations are based on angle coordinates. Rotation and transformation use angles as natural parameters.

Differential geometry

Curvature and torsion of curves are defined by angle changes. Circular angles are fundamental to the theory of curved spaces.

Oscillation theory

Harmonic oscillations are directly linked to circular motion. Phase angles and frequency analysis are based on circular angle concepts.

Quantum mechanics

Quantum phases and probability amplitudes use complex angle functions developed from classical circular angles.

Summary

Circular angles represent one of the most elegant connections between elementary geometry and higher mathematics. The fundamental relation θ = μ/2 is not only a practical calculation formula but an expression of deep geometric symmetry. From ancient astronomy to modern robotics, from GPS navigation to quantum physics - circular angles form an indispensable mathematical foundation. Their importance goes far beyond pure geometry and makes them a central tool for engineers, physicists and mathematicians. In an increasingly technical world where precision and automation are becoming ever more important, circular angles remain a fundamental and timeless mathematical concept.

Angle functions

From Deg, Min, Sec to Decimal • From Degree to Percent • Angle sum • Side lengths from angles

Circular functions

Annulus • Annulus sector • Circle • Circular angles • Circular arcs • Circular sector • Circular segment • Ellipse • Parabolic arch • Squaring the Circle