Circular Sector Calculator

Calculator and formulas for circular sector calculations (Circular Sector)

Circular Sector Calculator

The Circular Sector

A circular sector is a pie-shaped slice of a circle, bounded by two radii and an arc. Also called a "slice".

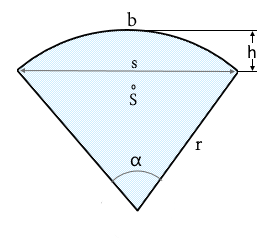
Enter Circular Sector Parameters
Radius of the circle
Which property is known?
Value of the selected property
Circular Sector Properties

Three boundaries: Two radii plus one arc

Radius r Central Angle α Arc Chord
Circular Sector Calculation Results
Angle α:
Area A:
Perimeter P:
Arc length b:
Chord s:
Centroid S:
Height h:

Circular Sector Structure

A circular sector is like a pie slice.
Bounded by two radii and an arc.

Circular Sector

What is a Circular Sector?

A circular sector is one of the most fundamental shapes in circle geometry:

  • Definition: Pie-shaped slice of a circle
  • Three boundaries: Two radii plus one arc
  • Central angle: Angle α between the two radii
  • Proportionality: All properties proportional to α
  • Versatile shape: From narrow wedge to almost full circle
  • Practical relevance: Basis for charts and measuring devices

Geometric Properties of the Circular Sector

The circular sector has characteristic geometric properties:

Basic Parameters
  • Radius r: Distance from center to circle line
  • Central angle α: Angle between the bounding radii
  • Arc: Curved boundary of the sector
  • Chord: Straight connection of arc endpoints
Special Properties
  • Proportionality: Area and arc ∝ central angle
  • Centroid: Lies on the angle bisector
  • Height: Distance from center to chord
  • Symmetry: Mirror symmetry about the angle bisector

Mathematical Relationships

The circular sector follows elegant mathematical laws:

Area Calculation
A = πr² · α/360°

The sector area is proportional to the central angle. Fraction of circle area corresponds to fraction of the angle.

Arc Length
b = πr · α/180°

The arc is proportional to radius and angle. In radians the formula simplifies to b = rα.

Applications of Circular Sectors

Circular sectors are versatile:

Data Visualization
  • Pie charts and donut charts
  • Dashboards and KPI displays
  • Progress wheels
  • Gauges and instruments
Engineering & Technology
  • Valves and flaps
  • Rotary switches and potentiometers
  • Turbine blades and propellers
  • Gear segments and couplings
Architecture & Design
  • Window shapes and stairwell designs
  • Dome sections and vaults
  • Amphitheater and stadium sections
  • Landscape architecture
Art & Graphics
  • Logo design and corporate identity
  • Ornaments and decorative elements
  • User interface design
  • Ceramics and glass art

Formulas for the Circular Sector

Area A
\[A = \pi r^2 \cdot \frac{\alpha}{360°}\]

Sector area proportional to the central angle

Arc length b
\[b = \pi r \cdot \frac{\alpha}{180°}\]

Arc length proportional to radius and angle

Perimeter P
\[P = 2r + b\]

Two radii plus arc

Chord s
\[s = 2r \sin\left(\frac{\alpha}{2}\right)\]

Trigonometric relation to half the central angle

Centroid S
\[S = \frac{2}{3} \cdot \frac{r \cdot \sin(\alpha/2)}{\alpha/180° \cdot \pi}\]

Distance of the centroid from the center

Height h
\[h = r - r\cos\left(\frac{\alpha}{2}\right)\]

Distance from center to the chord

Central Angle α (from area)
\[\alpha = \frac{360° \cdot A}{\pi r^2}\]

Recompute the angle from the area

Central Angle α (from chord)
\[\alpha = 2 \arcsin\left(\frac{s}{2r}\right)\]

Recompute the angle from the chord

Calculation Example for a Circular Sector

Given
Radius r = 12 Central Angle α = 60°

Find: All properties of the 60° sector (one sixth of the circle)

1. Area and Arc Length
\[A = \pi \times 12^2 \times \frac{60°}{360°} = 75.40\] \[b = \pi \times 12 \times \frac{60°}{180°} = 12.57\]

One sixth of the circle area and circumference

2. Chord and Perimeter
\[s = 2 \times 12 \times \sin(30°) = 12.00\] \[P = 2 \times 12 + 12.57 = 36.57\]

At 60° the chord equals the radius!

3. Centroid and Height
\[S = \frac{2}{3} \times \frac{12 \times 0.5}{\pi/3} = 5.73\] \[h = 12 - 12 \cos(30°) = 1.61\]

Centroid and distance to the chord

4. Special 60° Properties
\[\text{Chord} = \text{Radius} = 12\] \[\text{Equilateral triangle!}\]

The 60° sector forms an equilateral triangle

5. Complete 60° Sector
Radius r = 12.00 Central Angle α = 60° Area A = 75.40 Arc length b = 12.57
Chord s = 12.00 = r Perimeter P = 36.57 Centroid S = 5.73 Height h = 1.61

A special sector - together with the center it forms an equilateral triangle

The Circular Sector: Building Block of Circle Geometry

The circular sector is one of the most fundamental and versatile geometric shapes. As a "pie slice" of the circle it connects elementary geometry with practical applications and is ubiquitous in modern data visualization, engineering and architecture.

Definition and Geometric Structure

The circular sector is characterized by elegant simplicity:

  • Triple boundary: Two radii from the center plus an arc
  • Angle dependence: All properties directly proportional to the central angle α
  • Scalability: Shape preserved under scaling
  • Symmetry: Mirror symmetry about the angle bisector
  • Continuous transition: From infinitesimal wedge to almost full circle

Mathematical Elegance and Proportionality

The mathematics of the circular sector is notable for its clarity:

Proportionality principle

All key properties (area, arc length) are directly proportional to the central angle. This makes computations intuitive and predictable.

Trigonometric connections

The chord formula s = 2r·sin(α/2) connects the sector elegantly with trigonometry and shows the fundamental role of the sine.

Centroid calculation

The centroid always lies on the angle bisector at a distance of 2r·sin(α/2)/(3·α) from the center - a remarkable geometric constant.

Limit behavior

For small angles the sector approaches a triangle, for large angles it approaches the full circle - important for approximations.

Modern Applications and Data Visualization

In the digital age the circular sector has experienced a renaissance:

Data visualization

Pie charts use sectors for intuitive representation of shares. Angles directly correspond to data values - a natural proportion display.

Interactive Interfaces

Modern UIs use sectors for progress displays, menus and controls - from mobile apps to industrial dashboards.

Measuring instruments

Analogue and digital instruments (tachometers, manometers) use sectors for precise and readable displays.

Gaming and VR

Games and virtual reality applications use sector-based interfaces for natural circular menu navigation and status displays.

Technical and Architectural Applications

Circular sectors are essential in practical applications:

  • Mechanical engineering: Valves, flaps and rotary switches use sector geometry for precise opening angles
  • Turbine technology: Blades and rotors follow sector principles for optimal flow
  • Architecture: Domes, stairs and amphitheaters use sector sections for structure and aesthetics
  • Optics: Segmented mirrors and lenses in telescopes are based on sector geometry
  • Electronics: Rotary capacitors and potentiometers use variable sector overlap

Special Angles and Their Properties

Certain angles yield especially elegant properties:

60° (π/3) - The harmonic sector

At 60° the chord equals the radius, forming an equilateral triangle. Useful in constructive applications.

90° (π/2) - The quarter circle

The right-angled sector is fundamental for coordinate systems and technical constructions. Its chord equals r√2.

180° (π) - The semicircle

The largest proper sector becomes a semicircle with the straight chord as diameter. Fundamental for many constructions.

120° (2π/3) - The third circle

Three such sectors form a full circle - important for symmetric designs and triple-split applications.

Summary

The circular sector embodies geometric elegance in pure form. Its simple definition - a slice between two radii - hides a rich mathematical structure with direct proportionalities and elegant trigonometric relations. From ancient astronomical computations to modern data visualization, the circular sector remains a fundamental tool for intuitive representation of shares and angles. Its versatility - from tiny UI elements to monumental architecture - demonstrates the timeless relevance of basic geometric principles. In a data-driven world where visual communication matters, the circular sector remains indispensable for designers, engineers and mathematicians.

Angle functions

From Deg, Min, Sec to Decimal • From Degree to Percent • Angle sum • Side lengths from angles

Circular functions

Annulus • Annulus sector • Circle • Circular angles • Circular arcs • Circular sector • Circular segment • Ellipse • Parabolic arch • Squaring the Circle