Circular Arc Calculator

Calculator and formulas for circular arc calculations

Circular Arc Calculator

The Circular Arc

A circular arc is a curved circle segment with a specific radius and angle. Length, chord and angle are directly related.

Enter Two Known Parameters
Select the first known parameter
Value of the first parameter
Select the second known parameter
Value of the second parameter
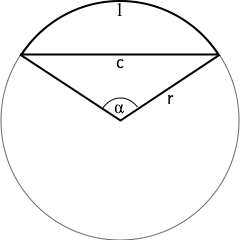
Circular Arc Properties

Circle segment: Part of a circle between two radii

Radius r Angle α Arc length l Chord c
Circular Arc Calculation Results
Angle α:
Radius r:
Chord c:
Arc l:

Circular Arc Structure

A circular arc connects radius, angle, arc length and chord.
The arc length is proportional to the central angle.

Circular Arc

What is a Circular Arc?

A circular arc is a fundamental element of circle geometry:

  • Definition: Part of the circle between two points
  • Central angle: Angle α between the two radii
  • Arc length: Length l of the curved segment
  • Chord: Straight connection between endpoints
  • Sector: Area enclosed by the arc
  • Proportionality: Arc proportional to the angle

Geometric Properties of the Circular Arc

The circular arc exhibits characteristic geometric relationships:

Basic Parameters
  • Radius r: Distance from center to any arc point
  • Central angle α: Angle between bounding radii
  • Arc length l: Length along the circle
  • Chord c: Direct connection of endpoints
Special Relations
  • Proportionality: Arc length ∝ central angle
  • Relation to full circle: l/2πr = α/360°
  • Chord relation: Chord is shorter than arc length
  • Symmetry: Arc symmetric about angle bisector

Mathematical Relationships

The circular arc follows precise mathematical laws:

Arc Length
l = 2πr · α/360°

The arc length is proportional to the central angle. Fraction of the full circle equals fraction of 360°.

Chord
c = 2r · sin(α/2)

The chord connects the arc endpoints directly. Relation via trigonometry of half the central angle.

Applications of Circular Arcs

Circular arcs have a wide range of practical applications:

Mechanical & Engineering
  • Cams and cam profiles
  • Gears and tooth profiles
  • Guide rails and sliding paths
  • Hydraulic and pneumatic systems
Architecture & Construction
  • Arches, vaults and domes
  • Stairs and spiral staircases
  • Bridges and bridge arches
  • Window and door arches
Transport & Navigation
  • Road curves and ramps
  • Railway curves and switches
  • Aircraft turns and approach paths
  • Marine routes and harbor entries
Design & Art
  • Ornaments and decorative elements
  • Furniture design and fillets
  • Logo design and graphics
  • Watches, dials and scales

Formulas for the Circular Arc

Arc Length l
\[l = 2\pi r \cdot \frac{\alpha}{360°} = \frac{\pi r \alpha}{180°}\]

Proportional to radius and angle

Chord c
\[c = 2r \cdot \sin\left(\frac{\alpha}{2}\right)\]

Trigonometric relation to half the angle

Central Angle α
\[\alpha = \frac{360° \cdot l}{2\pi r} = 2 \cdot \arcsin\left(\frac{c}{2r}\right)\]

Compute from arc length or chord

Radius r
\[r = \frac{l \cdot 180°}{\pi \alpha} = \frac{c}{2 \sin(\alpha/2)}\]

From arc/angle or chord/angle

Sector Area A
\[A = \frac{\pi r^2 \alpha}{360°} = \frac{r \cdot l}{2}\]

Area of the sector enclosed by the arc

Arc-Chord Ratio
\[\frac{l}{c} = \frac{\alpha/2}{\sin(\alpha/2)} \text{ for } \alpha \text{ in radians}\]

Ratio always ≥ 1 (arc longer than chord)

Calculation Example for a Circular Arc

Given
Radius r = 15 Central Angle α = 90°

Find: Arc length and chord of the quarter circle

1. Compute Arc Length
\[l = 2\pi \times 15 \times \frac{90°}{360°}\] \[l = 2\pi \times 15 \times 0.25 = 23.56\]

Quarter of the circle circumference

2. Compute Chord
\[c = 2 \times 15 \times \sin(45°)\] \[c = 30 \times 0.707 = 21.21\]

Diagonal of the square with side length r

3. Sector Area
\[A = \frac{\pi \times 15^2 \times 90°}{360°}\] \[A = \frac{706.86}{4} = 176.71\]

Quarter of the circle area

4. Check Ratios
\[\frac{l}{c} = \frac{23.56}{21.21} = 1.11\] \[\frac{l}{2\pi r} = \frac{90°}{360°} = 0.25\]

Arc is 11% longer than chord

5. Complete Circular Arc
Radius r = 15.00 Angle α = 90° Arc length l = 23.56
Chord c = 21.21 Sector Area A = 176.71 Quarter circle!

A classic 90° quarter-circle arc with all calculated properties

The Circular Arc: Basis of Curved Geometry

The circular arc is a fundamental element of geometry and a starting point for understanding curved shapes. From ancient architecture to modern engineering it underlies countless constructions and mathematical concepts.

Definition and Fundamental Properties

The circular arc connects elementary geometry with advanced mathematics:

  • Geometric definition: Part of the circle between two points, defined by radius and central angle
  • Parametric representation: Fully described by three parameters: radius, start angle and central angle
  • Intrinsic curvature: Constant curvature κ = 1/r makes the circular arc the simplest curved line
  • Proportionality principle: Arc length is directly proportional to the central angle (for fixed radius)
  • Universal scaling: All geometric relations remain under scaling

Trigonometric Relations and Analysis

The circular arc is closely linked to trigonometry:

Sine and Cosine

The chord of a circular arc is directly related to the sine of the half central angle. This connection makes the circular arc the geometric origin of trigonometric functions.

Radian measure

Radian measure defines angles via arc length/radius. A full circle equals 2π radians, the natural unit for angles in analysis.

Limit considerations

For small angles the arc length approaches the chord: lim(α→0) l/c = 1. This limit is fundamental for differential calculus of curved functions.

Series expansions

Trigonometric functions can be represented as power series whose geometric interpretation is through circular arcs - a bridge between geometry and analysis.

Historical Significance and Development

The circular arc has a rich mathematical history:

Ancient mathematics

The Greeks recognized the significance of arcs for architecture and astronomy. Hippocrates of Chios studied the quadrature of lunes formed by circular arcs.

Medieval development

Islamic mathematicians such as Al-Battani refined arc calculations for astronomical purposes and laid foundations for trigonometry.

Renaissance and Baroque

Systematic investigation of curves by Descartes, Fermat and Newton led to analytic geometry and calculus.

Modern mathematics

Today arcs are fundamental to differential geometry, complex analysis and numerical mathematics - from computer graphics to theoretical physics.

Technical Applications and Engineering

Circular arcs are indispensable in modern engineering:

  • Mechanical engineering: Cams, profiles and guide paths use arcs for precise predictable motion
  • Transport engineering: Road and railway curves follow arcs for optimal dynamics and safety
  • Architecture: Arches and vaults use arc properties for stability and aesthetics
  • Computer graphics: Arcs are basic elements for splines and vector drawing
  • Robotics: Motion planning uses arcs for smooth natural movements
  • Optics: Spherical lenses and mirrors are based on arc geometry

Related Mathematical Concepts

The circular arc relates to many other mathematical objects:

Elliptic arcs

Generalization to elliptical arcs leads to elliptic integrals and richer mathematics.

Spline curves

Modern curve representations use circular arcs as building blocks for complex composed curves in CAD and graphics.

Hyperbolic geometry

In non-Euclidean geometries there are analogues to arcs with different curvature properties.

Fractal curves

Some fractals are approximated by ever finer circular arcs, leading to interesting limit considerations.

Summary

The circular arc represents the elegant connection between elementary geometry and higher mathematics. Its simple definition - a piece of a circle - hides a wealth of mathematical relations that range from ancient trigonometry to modern differential geometry. As a building block of countless technical constructions and mathematical theories, the circular arc remains a timeless example of how fundamental geometric objects underpin complex applications. In a world of increasingly curved designs - from architecture to vehicle bodies to user interfaces - the circular arc is an indispensable tool to describe and construct elegant, functional shapes.

Angle functions

From Deg, Min, Sec to Decimal • From Degree to Percent • Angle sum • Side lengths from angles

Circular functions

Annulus • Annulus sector • Circle • Circular angles • Circular arcs • Circular sector • Circular segment • Ellipse • Parabolic arch • Squaring the Circle