Angle Degrees to Percent Calculator

Calculator and formula to convert angle degrees to percent and vice versa

Angle-Percent Converter

Angle-Percent conversion

Convert angles in degrees to percent (slope) or vice versa. The percentage represents the slope of a line.

Enter value
Note: Angle must be between -90° and +90°. 100% corresponds to 45°.
Enter the known value
Common angles
0°
Horizontal
30°
58%
45°
100%
60°
173%
Conversion result
Percent:
100% = 45° slope; values above 100% are possible

Slope visualization

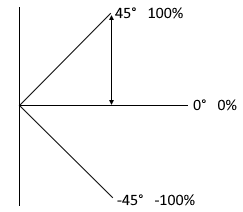
Angle Percent Diagram
Slope properties

Percentage = slope: ratio of rise to run

0° = 0% 45° = 100% 90° = ∞
Common conversions
Degrees Percent Description
0° 0% Horizontal
30° 57.7% Moderate slope
45° 100% Equal rise/run
60° 173.2% Steep slope
90° ∞ Vertical

Range: -90° < angle < +90°
Slope: Percent = tan(angle) × 100


Understanding angle-percent conversion

The angle-percent relationship describes the slope or gradient of a line:

  • Percent as slope: Rise divided by run, expressed as percentage
  • Tangent function: tan(angle) = opposite/adjacent = rise/run
  • 45° = 100%: Rise equals run (1:1 ratio)
  • Values > 100%: Angle > 45°, steep slopes
  • Road grades: 10% = 5.7° (common road slope)
  • Practical limit: tan(90°) → ∞ (vertical line)

Conversion formulas

Degrees to Percent
\[\text{Percent} = \tan(\text{Degrees}) \times 100\]

Uses tangent function to calculate slope percentage

Percent to Degrees
\[\text{Degrees} = \arctan\left(\frac{\text{Percent}}{100}\right)\]

Uses inverse tangent (arctan) to get angle

Slope definition
\[\text{Slope} = \frac{\text{Rise}}{\text{Run}} = \frac{\text{Vertical}}{\text{Horizontal}}\]

Basic definition of slope or gradient

Relation to tangent
\[\tan(\alpha) = \frac{\text{Opposite}}{\text{Adjacent}} = \frac{\text{Rise}}{\text{Run}}\]

Tangent connects angle to slope ratio

Calculation examples

Example 1: Degrees to Percent

Given: Angle = 30°

Find: Slope in percent

\[\text{Percent} = \tan(30°) \times 100\] \[= 0{,}577 \times 100\] \[= 57{,}7\%\]

Result: 30° corresponds to 57.7% slope

Example 2: Percent to Degrees

Given: Slope = 100%

Find: Angle in degrees

\[\text{Degrees} = \arctan\left(\frac{100}{100}\right)\] \[= \arctan(1{,}0)\] \[= 45°\]

Result: 100% slope corresponds to 45°

Example 3: Road grade

Given: Road grade = 10%

Find: Angle of incline

\[\text{Degrees} = \arctan\left(\frac{10}{100}\right)\] \[= \arctan(0{,}1)\] \[= 5{,}71°\]

Result: 10% grade = 5.71° angle

Example 4: Steep slope

Given: Angle = 60°

Find: Slope percentage

\[\text{Percent} = \tan(60°) \times 100\] \[= 1{,}732 \times 100\] \[= 173{,}2\%\]

Result: 60° is a very steep 173.2% slope

Geometric interpretation

The trigonometric relationship between angles and slopes:

Right triangle basis
  • Slope forms right triangle with horizontal
  • Tangent = opposite/adjacent sides
  • Angle determines steepness
  • Percent expresses ratio as percentage
Practical measurements
  • Road grades: typically 0-15% (0-8.5°)
  • Roof pitches: often 20-50% (11-27°)
  • Mountain slopes: can exceed 100%
  • Accessibility ramps: max 8.3% (4.8°)

Applications of angle-percent conversion

Angle-percent calculations are essential in many practical fields:

Civil Engineering
  • Road and highway design
  • Railroad track gradients
  • Drainage and sewer slopes
  • Accessibility ramp specifications
Architecture & Construction
  • Roof pitch calculations
  • Staircase design
  • Foundation grading
  • Water runoff management
Sports & Recreation
  • Ski slope classifications
  • Cycling hill categories
  • Running track banking
  • Skateboard ramp design
Surveying & Navigation
  • Topographic map interpretation
  • Land surveying and leveling
  • Terrain analysis
  • GPS elevation calculations

Mathematical foundations

The trigonometric basis of angle-percent conversion:

Tangent function
  • Periodic with period π (180°)
  • Range: (-∞, +∞)
  • Undefined at ±90° (vertical asymptotes)
  • Derivative: sec²(x)
Inverse tangent (arctan)
  • Principal range: (-90°, +90°)
  • Domain: all real numbers
  • Continuous and monotonic
  • Derivative: 1/(1 + x²)

Angle-percent conversion: bridging geometry and measurement

The angle-percent relationship elegantly connects abstract geometric angles with practical slope measurements. Through the tangent function, this conversion transforms angular measures into intuitive percentage expressions of steepness. From road engineering to architectural design, this fundamental trigonometric relationship enables precise quantification of inclines in everyday applications.

The power of trigonometric conversion

The angle-percent formula reveals key mathematical principles:

  • Tangent function: Natural bridge between angles and ratios
  • Percent as slope: Intuitive expression of steepness (rise/run × 100)
  • 45° = 100%: Critical point where rise equals run
  • Range limitation: Meaningful for angles between -90° and +90°
  • Asymptotic behavior: Approaches infinity as angle approaches ±90°
  • Practical utility: Converts abstract angles to measurable gradients
Summary

Angle-percent conversion demonstrates the practical power of trigonometry. The elegant formulas — tan(angle) × 100 for degrees to percent, and arctan(percent/100) for percent to degrees — transform theoretical geometry into everyday measurements. Whether designing roads, calculating roof pitches, or analyzing terrain, this fundamental relationship makes abstract angles tangible. It reminds us that mathematics bridges the gap between pure theory and practical application, turning geometric concepts into tools for engineering and design.

Angle functions

From Deg, Min, Sec to Decimal • From Degree to Percent • Angle sum • Side lengths from angles

Circular functions

Annulus • Annulus sector • Circle • Circular angles • Circular arcs • Circular sector • Circular segment • Ellipse • Parabolic arch • Squaring the Circle