Ellipse Calculator

Calculator and formulas for ellipses

Ellipse Calculator

The Ellipse

An ellipse is an oval, closed curve with two semi-axes: semi-major axis (a) and semi-minor axis (b).

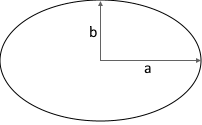
Enter Ellipse Parameters
Semi-axis in the longest direction
Semi-axis in the shortest direction
Ellipse Properties

Conic section: Obtained by an oblique cut through a cone

2 semi-axes 2 foci Oval shape
Ellipse Calculation Results
Perimeter P *):
Area A:

*) Perimeter computed via approximation (max. error 0.04%)

Ellipse Structure

An ellipse is an oval conic section with two semi-axes.
The semi-major axis (a) and semi-minor axis (b) determine the shape.

Ellipse

What is an Ellipse?

An ellipse is one of the most important geometric shapes and belongs to the conic sections:

  • Conic section: Obtained by an oblique cut of a cone
  • Closed curve: Oval, symmetric shape
  • Two semi-axes: Semi-major (a) and semi-minor (b)
  • Two foci: Characteristic property
  • Constant sum: Sum of distances to foci is constant
  • Versatile applications: Nature, engineering, astronomy

Geometric Properties of the Ellipse

The ellipse has fascinating geometric properties:

Axes and Symmetry
  • Semi-major axis (a): Longest distance from center
  • Semi-minor axis (b): Shortest distance from center
  • Two symmetry axes: Major and minor axes
  • Center: Intersection point of the axes
Foci
  • Two foci (F₁, F₂): Characteristic for ellipses
  • Distance from center: c = √(a² - b²)
  • Constant sum: |PF₁| + |PF₂| = 2a for all points P
  • Eccentricity: e = c/a (0 ≤ e < 1)

Mathematical Relationships

The ellipse follows precise mathematical laws:

Area Calculation
A = π · a · b

Area is the product of the two semi-axes times π. For a circle (a = b = r) this reduces to πr².

Perimeter Approximation
P ≈ π(a+b)(1 + 3λ²/(10+√(4-3λ²)))

Perimeter requires an approximation with λ = (a-b)/(a+b). Maximum error: 0.04%

Applications of the Ellipse

Ellipses are ubiquitous in nature, technology and art:

Astronomy & Physics
  • Planetary orbits around the sun
  • Comet orbits in the solar system
  • Satellite orbits around planets
  • Elliptical galaxy shapes
Architecture & Engineering
  • Vault shapes and arches
  • Stadiums and amphitheaters
  • Optical lenses and mirrors
  • Gear and cam profiles
Art & Design
  • Perspective representations of circles
  • Ornaments and decorative elements
  • Logo design and graphics
  • Artworks with elliptical shapes
Nature & Biology
  • Leaf shapes and botanical structures
  • Bird eggs and organic forms
  • Cell structures in microbiology
  • Crystal growth and mineral shapes

Formulas for the Ellipse

Area A
\[A = \pi \cdot a \cdot b\]

Simple formula: π times both semi-axes

Perimeter P (approximation)
\[P = \pi(a+b)\left(1 + \frac{3\lambda^2}{10+\sqrt{4-3\lambda^2}}\right)\]

With λ = (a-b)/(a+b), error max. 0.04%

Focal distance c
\[c = \sqrt{a^2 - b^2}\]

Distance of foci from the center

Eccentricity e
\[e = \frac{c}{a} = \frac{\sqrt{a^2 - b^2}}{a}\]

Measure of flattening (0 ≤ e < 1)

Ellipse equation (cartesian)
\[\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1\]

Standard form for the ellipse in coordinates

Parametric form
\[x = a \cos(t), \quad y = b \sin(t)\]

With parameter t ∈ [0, 2π]

Calculation Example for an Ellipse

Given
Semi-major a = 8 Semi-minor b = 5

Find: All geometric properties of the ellipse

1. Basic calculations
\[A = \pi \times 8 \times 5 = 125.66\] \[\lambda = \frac{8-5}{8+5} = 0.231\]

Area and λ-parameter

2. Perimeter calculation
\[P = \pi \times 13 \times 1.017 = 41.53\]

Approximation formula applied

3. Foci
\[c = \sqrt{64 - 25} = 6.24\] \[e = \frac{6.24}{8} = 0.78\]

Focal distance and eccentricity

4. Ellipse equation
\[\frac{x^2}{64} + \frac{y^2}{25} = 1\]

Standard form of the ellipse equation

5. Complete ellipse
Semi-axis a = 8.00 Semi-axis b = 5.00 Area A = 125.66
Perimeter P = 41.53 Eccentricity e = 0.78 Foci ±6.24

A distinctly elliptical shape with moderate eccentricity

The Ellipse: Fundamental Curve of Geometry

The ellipse is one of the most significant curves in mathematics and the natural sciences. As a conic section it links elementary geometry with higher mathematics and finds countless applications from planetary mechanics to modern engineering.

The ellipse as a conic section

The ellipse belongs to the four classical conic sections and arises in a special way:

  • Origin: Oblique cut through a circular cone (angle between cone surface and cut plane < 90°)
  • Closed curve: Unlike parabola and hyperbola it is bounded
  • Continuous transition: From circle (e=0) to parabola (e=1)
  • Projective property: Every circle is an ellipse in perspective projection
  • Affine invariance: Ellipses are preserved under affine transforms

The focus property: Heart of the ellipse

The characteristic property of the ellipse is based on its two foci:

Mathematical definition

For each point P on the ellipse the sum of the distances to both foci F₁ and F₂ is constant: |PF₁| + |PF₂| = 2a. This property makes the ellipse constructible and computable.

Gardener's construction

Using a string of length 2a attached to two pins (the foci) one can draw a perfect ellipse - a practical demonstration of the focus property.

Physical significance

In optics rays reflected from one focus are directed to the other (elliptical mirrors); in acoustics "whispering galleries" arise from this property.

Astronomical relevance

Planetary orbits follow elliptical curves with the sun at one focus - a fundamental insight of celestial mechanics since Kepler.

Mathematical challenges and solutions

The ellipse poses interesting mathematical problems:

The perimeter problem

Unlike the simple area formula A = πab, the perimeter of an ellipse is not elementary. It requires elliptic integrals or approximations such as Ramanujan's approximation used here.

Parametric representation

The parametric form x = a·cos(t), y = b·sin(t) enables elegant calculations and is fundamental for computer graphics and numerical methods.

Eccentricity as shape measure

The eccentricity e = c/a characterizes the flattening of the ellipse: e = 0 gives a circle, e → 1 a very flat ellipse.

Coordinate transformations

Ellipses in arbitrary orientation require rotation and translation matrices, which makes them important objects in linear algebra.

Applications in science and engineering

The ellipse is far more than a geometric curiosity:

  • Astronomy: Planetary and cometary orbits, satellite trajectories per Kepler's laws
  • Optics: Elliptical mirrors and lenses, laser resonators, telescope systems
  • Acoustics: Concert halls with elliptical ceilings, whispering galleries
  • Mechanical engineering: Elliptical gears, cam mechanisms, eccentric disks
  • Architecture: Dome constructions, bridge arches, stadium shapes
  • Statistics: Confidence ellipses in multivariate data analysis
Summary

The ellipse embodies the perfect combination of geometric elegance and practical applicability. From its definition via two foci to its role in celestial mechanics, it shows how mathematical structures permeate the physical world. Its apparent simplicity hides deep mathematical connections, ranging from elementary geometry to complex elliptic integrals. In a world increasingly driven by precision and efficiency, the ellipse remains a fundamental tool for engineers, physicists and mathematicians — a timeless example of how beauty and function are inseparably linked in mathematics.

Angle functions

From Deg, Min, Sec to Decimal • From Degree to Percent • Angle sum • Side lengths from angles

Circular functions

Annulus • Annulus sector • Circle • Circular angles • Circular arcs • Circular sector • Circular segment • Ellipse • Parabolic arch • Squaring the Circle