Annulus Sector Calculator

Calculator and formulas for annulus sector calculations

Annulus Sector Calculator

The Annulus Sector

An annulus sector is a section of an annulus, bounded by two radii and an angle. Combination of annulus and circular sector.

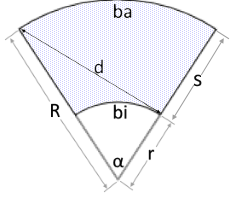
Enter Annulus Sector Parameters
Radius of the outer circle
Radius of the inner circle
Central angle in degrees
Annulus Sector Properties

Double Boundary: Bounded by radii (ring) and angle (sector)

Outer Radius R Inner Radius r Central Angle α
Annulus Sector Calculation Results
Area A:
Perimeter P:
Side Length s:
Outer Arc ba:
Inner Arc bi:
Diagonal d:

Annulus Sector Structure

An annulus sector combines ring and sector geometry.
Bounded by two radii, one angle, and two circular arcs.

Annulus Sector

What is an Annulus Sector?

An annulus sector is a complex geometric form with multiple boundaries:

  • Definition: Section of an annulus with angular limitation
  • Dual Structure: Combination of ring and sector
  • Four Boundaries: Two radii, two circular arcs
  • Three Parameters: Outer radius R, inner radius r, angle α
  • Complex Geometry: Diverse calculation formulas
  • Practical Form: Common in engineering and architecture

Geometric Properties of the Annulus Sector

The annulus sector unifies properties of ring and sector:

Basic Parameters
  • Outer Radius R: Defines the outer boundary of the sector
  • Inner Radius r: Defines the inner boundary of the sector (r < R)
  • Central Angle α: Angular limitation of the sector
  • Side Length s: s = R - r (radial extent)
Special Properties
  • Two Circular Arcs: Outer arc ba and inner arc bi
  • Two Straight Sides: Radial boundary lines
  • Proportionality: Area proportional to α, R² - r²
  • Diagonal: Connects opposite vertices

Mathematical Relationships

The annulus sector follows complex mathematical rules:

Area Calculation
A = π(R² - r²) · α/360°

Fraction of the annulus area according to the angle. Combination of ring and sector formula.

Perimeter Calculation
P = π(R+r)·α/180° + 2(R-r)

Sum of both circular arcs plus both radial sides.

Applications of Annulus Sectors

Annulus sectors have specialized practical applications:

Mechanical Engineering
  • V-belt pulleys and couplings
  • Brake discs and clutch plates
  • Cam discs and curve discs
  • Transmission and engine components
Architecture & Construction
  • Vault and dome sections
  • Stairs and spiral staircases
  • Window and door arches
  • Amphitheater and stadium sections
Data Visualization
  • Donut charts and ring diagrams
  • Gauges and measuring instruments
  • Clocks and time displays
  • Progress indicators (progress rings)
Design & Art
  • Logos and graphic elements
  • Ornaments and decorations
  • Ceramics and glass art
  • Jewelry and decorations

Formulas for the Annulus Sector

Area A
\[A = \pi(R^2 - r^2) \cdot \frac{\alpha}{360°}\]

Fraction of the annulus area according to central angle

Perimeter P
\[P = \pi(R + r) \cdot \frac{\alpha}{180°} + 2(R - r)\]

Both circular arcs plus both radial sides

Side Length s
\[s = R - r\]

Radial extent of the sector

Outer Arc ba
\[b_a = \pi R \cdot \frac{\alpha}{180°}\]

Circular arc of the outer radius

Inner Arc bi
\[b_i = \pi r \cdot \frac{\alpha}{180°}\]

Circular arc of the inner radius

Diagonal d
\[d = \sqrt{R^2 + r^2 - 2Rr\cos(\alpha)}\]

Law of cosines for the triangle between the radii

Calculation Example for an Annulus Sector

Given
Outer Radius R = 15 Inner Radius r = 10 Central Angle α = 120°

To find: All properties of the annulus sector

1. Basic Calculations
\[s = 15 - 10 = 5\] \[\frac{\alpha}{360°} = \frac{120°}{360°} = \frac{1}{3}\]

Side length and angle factor

2. Area Calculation
\[A = \pi(15^2 - 10^2) \cdot \frac{1}{3}\] \[A = \pi \cdot 125 \cdot \frac{1}{3} = 130.90\]

One third of the ring area

3. Calculate Circular Arcs
\[b_a = \pi \cdot 15 \cdot \frac{120°}{180°} = 31.42\] \[b_i = \pi \cdot 10 \cdot \frac{120°}{180°} = 20.94\]

Outer and inner circular arcs

4. Perimeter and Diagonal
\[P = 31.42 + 20.94 + 2 \cdot 5 = 62.36\] \[d = \sqrt{15^2 + 10^2 - 300 \cos(120°)} = 21.79\]

Total perimeter and diagonal

5. Complete Annulus Sector
Outer Radius R = 15.00 Inner Radius r = 10.00 Central Angle α = 120° Side Length s = 5.00
Area A = 130.90 Perimeter P = 62.36 Outer Arc = 31.42 Diagonal d = 21.79

A 120° annulus sector - one third of the full ring

The Annulus Sector: Complex Geometry Simplified

The annulus sector is one of the most versatile geometric forms, elegantly combining ring and sector geometries. As a section of an annulus with angular limitation, it finds application in numerous technical and design fields, from machine components to modern data visualizations.

Definition and Structural Complexity

The annulus sector unifies the properties of two fundamental geometric objects:

  • Ring Properties: Concentric circles with outer radius R and inner radius r
  • Sector Properties: Angular limitation by central angle α and two radial lines
  • Four Boundaries: Two circular arcs (outer and inner) plus two straight radii
  • Three Parameters: Fully characterized by R, r, and α
  • Double Symmetry: Mirror symmetry respecto to the angle bisectors

Mathematical Challenges and Solutions

The mathematical treatment of annulus sectors requires the combination of different approaches:

Area Integration

The area can be calculated as the difference of circular sector areas or by polar coordinate integration: A = ∫∫ r dr dφ with suitable limits.

Perimeter Complexity

The perimeter consists of four different components: two circular arcs of different radii and two straight sections in the radial direction.

Diagonal Calculation

The diagonal requires the law of cosines: d = √(R² + r² - 2Rr·cos(α)). This formula elegantly connects all three parameters in a single relationship.

Limit Considerations

For r → 0, the sector becomes a simple circular sector; for α → 360°, it becomes a full ring - important special cases for verification.

Technical Applications and Design Principles

Annulus sectors are essential in modern technology and design:

Mechanical Engineering Applications

Brake discs, clutch plates, and V-belt pulleys utilize annulus sector geometry for optimal power transmission and heat dissipation. The form allows large contact areas in a compact design.

Architectural Elements

Vault segments, stairs, and amphitheater sections follow annulus sector geometry. The form combines structural stability with aesthetic elegance.

Modern Data Visualization

Donut charts, gauges, and progress rings use annulus sectors for intuitive data representation. The form enables multi-layered information delivery in a compact space.

Optics and Electronics

Sector apertures in cameras and segmented displays use precise annulus sector geometry for functional and aesthetic purposes.

Optimization Problems and Mathematical Applications

Annulus sectors offer interesting optimization possibilities:

  • Material Optimization: Minimal perimeter for a given area or maximal area for a given perimeter
  • Structural Mechanics: Optimal R/r ratios for minimal stress concentrations
  • Manufacturing Aspects: Angular ranges that allow efficient manufacturing processes
  • Functional Integration: Combination of several annulus sectors for complex technical functions
  • Aesthetic Proportions: Golden ratio and other harmonic proportions in design

Related Geometric Concepts

The annulus sector is related to other mathematical objects:

Elliptical Sectors

Generalization to elliptical rings and their sectors leads to more complex mathematics, but also to more versatile applications in technology.

3D Extensions

Spherical sectors and toroidal sections extend the concept into three-dimensional space - important for architecture and mechanical engineering.

Complex Analysis

Annulus sectors correspond to special areas in the complex plane, making them interesting for function theory and conformal mappings.

Numerical Methods

The discretization of annulus sectors is fundamental for finite element methods and computer graphics algorithms.

Summary

The annulus sector impressively demonstrates how the combination of simple geometric concepts leads to a rich, versatile form. Its mathematical elegance - characterized by just three parameters - conceals a complex structure with quadruple boundaries and diverse calculation formulas. From classic mechanical engineering applications to modern interface designs, the annulus sector shows its timeless relevance. The challenge of its mathematical treatment - from area integration to optimization problems - makes it an ideal object for understanding advanced geometric concepts. In an increasingly digitalized world, where data visualization and user-friendly interfaces are gaining importance, the annulus sector remains a fundamental tool for designers, engineers, and mathematicians.

Angle functions

From Deg, Min, Sec to Decimal • From Degree to Percent • Angle sum • Side lengths from angles

Circular functions

Annulus • Annulus sector • Circle • Circular angles • Circular arcs • Circular sector • Circular segment • Ellipse • Parabolic arch • Squaring the Circle