Parabolic Arch Calculator
Calculator and formulas for parabolic arch calculations
Parabolic Arch Calculator
The Parabolic Arch
A parabolic arch is a curved segment of a parabola, bounded by height and chord. Basic shape for many bridges and arches.
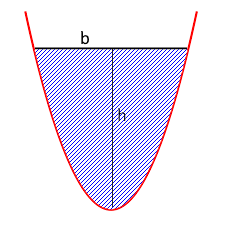
Parabolic Arch Structure
A parabolic arch is an efficient form for bridges.
Even force distribution and elegant curve.
|
|
What is a Parabolic Arch?
A parabolic arch is a segment of a parabola with special properties:
- Definition: Curved portion of a parabola
- Parameters: Height h and chord b characterize the shape
- Optimal curve: Even load distribution
- Structural relevance: Ideal for bridges and arches
- Mathematical elegance: Simple quadratic function
- Practical use: Architecture to physics
Geometric Properties of the Parabolic Arch
The parabolic arch has characteristic geometric properties:
Basic Parameters
- Height h: Maximum distance from the chord
- Chord b: Horizontal base line of the arch
- Arc length L: Length of the curved line
- Shape parameter s: s = √(b² + 16h²)
Special Properties
- Symmetry: Mirror symmetry about the midline
- Optimal curve: Minimal material for max strength
- Force distribution: Even load uptake
- Simple formula: y = 4h/b² · x(b-x)
Mathematical Relationships
The parabolic arch follows elegant mathematical laws:
Area Calculation
Two thirds of the rectangle area h·b. Simple and elegant integral result.
Arc Length
Complex formula with logarithm. Result of arc-length integration.
Applications of Parabolic Arches
Parabolic arches are essential in many fields:
Bridge Building & Architecture
- Arch bridges and viaducts
- Domes and vault constructions
- Hangars and sports halls
- Tunnels and underpasses
Technology & Physics
- Parabolic mirrors and satellite dishes
- Headlights and reflector systems
- Solar collectors and concentrators
- Radio telescopes and antennas
Hydraulics & Water Engineering
- Dams and weirs
- Channel cross-sections
- Overflow channels and plunge pools
- Water storage and cisterns
Transport Infrastructure
- Highway bridges and overpasses
- Railway viaducts
- Road tunnels and subway tubes
- Pedestrian bridges
Formulas for the Parabolic Arch
Area A
Two thirds of the enclosing rectangle area
Arc length L
Complex formula with logarithm and shape parameter s
Shape parameter s
Auxiliary value for the arc-length calculation
Parabola function y(x)
Quadratic function of the parabolic arch
Vertex form
Parabola with vertex at (b/2, h)
Ratio A/A_rectangle
Parabolic arch occupies 2/3 of the rectangle
Calculation Example for a Parabolic Arch
Given
Find: Area and arc length of the parabolic arch
1. Compute area
Simple computation: 2/3 of the rectangle area
2. Compute shape parameter s
Auxiliary value for the arc length
3. Log term
Logarithm for the arc-length formula
4. Compute arc length
Complex computation with logarithm
5. Complete parabolic arch
A classic parabolic arch with height-to-width ratio 2:3
The Parabolic Arch: Optimal Curve in Nature and Engineering
The parabolic arch is one of the most elegant and practical curve forms in mathematics and engineering. As a quadratic function it embodies mathematical simplicity while offering optimal structural properties for bridges, arches and physical applications.
Mathematical foundations and historical development
The parabola and its arches have a rich mathematical history:
- Ancient discoveries: Archimedes computed parabola areas with geometric methods
- Conic theory: Apollonius classified the parabola as a fundamental conic section
- Integral calculus: Leibniz and Newton used parabolas for early integration problems
- Physical applications: Galileo recognized parabolic trajectories in ballistics
- Modern engineering: Parabolic mirrors and optimized arch designs
Structural superiority and engineering applications
Parabolic arches possess unique structural advantages:
Optimal load distribution
Under uniform load the parabolic line matches the moment line, leading to minimal bending stresses and maximum efficiency. Bridge engineers exploit this for optimized designs.
Material efficiency
The parabola y = 4h/b²·x(b-x) minimizes material required for a given span and capacity. This makes parabolic arches ideal for long spans.
Constructive simplicity
The simple quadratic form allows precise calculation and cost-effective fabrication. Formwork can be generated from basic formulas.
Aesthetic effect
The harmonious curve of the parabolic arch is widely appreciated aesthetically and shapes architecture from antiquity to modern times.
Physical principles and optimization theory
The parabola is fundamentally linked to physical laws:
Gravity trajectories
Projectiles follow parabolic paths under gravity. This physical law makes parabolic arches a natural form for force-optimized structures.
Catenary approximation
Under uniform load the hanging chain (catenary) approximates a parabola. This explains the efficiency of parabolic arches in structural design.
Reflection properties
Parabolic mirrors focus parallel rays to a focal point — fundamental for telescopes, satellite dishes and solar concentrators.
Optimization problems
Many optimization problems yield parabolic solutions: minimal surfaces, shortest times, least energy — the parabola is a natural optimal curve.
Modern technical applications
Parabolic arches are essential in modern engineering:
- Bridge engineering: Highway and railway bridges with spans over 500m
- Aerospace: Parabolic antennas for satellite communication and deep-space contact
- Energy: Solar concentrators and parabolic trough power plants
- Acoustics: Parabolic reflectors for directional microphones and speaker systems
- Optics: Telescope mirrors and automotive headlights with parabolic reflectors
- Architecture: Modern domes and roofs with large spans
Computation aspects and numerical methods
Computing parabolic arches exposes interesting mathematical aspects:
Area integration
The area A = (2/3)hb follows from integration ∫₀ᵇ y(x)dx = ∫₀ᵇ (4h/b²)x(b-x)dx. A classic polynomial integration example.
Arc-length computation
The complex formula L = s/2 + (b²/8h)ln((4h+s)/b) results from the integral ∫√(1+(dy/dx)²)dx — a challenging analytical problem.
Numerical approximation
For practical use Simpson's rule or Gaussian quadrature are often used to compute arc lengths and moments numerically.
CAD integration
Modern CAD systems use NURBS and Bézier curves, which build on parabolic principles for precise technical drawings.
Future directions and research
Current research expands parabolic-arch applications:
- Biomimetics: Natural parabolic forms in plants and animals as inspiration for engineering designs
- Smart materials: Adaptive parabolic structures that change curvature
- Nano-technology: Parabolic structures at molecular scale for optics and electronics
- Space technology: Deployable parabolic antennas for satellites and probes
- Renewables: Optimized parabolic collectors for highest solar efficiency
Summary
The parabolic arch unites mathematical elegance and practical functionality. Its simple quadratic definition y = 4h/b²·x(b-x) hides a rich structure of optimal properties that make it a top choice for bridges, reflectors and load-bearing structures. From Archimedes' geometric proofs to modern satellite antenna systems the parabola remains a timeless mathematical and engineering tool. The elegant area formula A = (2/3)hb and the complex arc-length integral demonstrate mathematical depth while countless practical applications confirm the enduring relevance of this fundamental curve.
|
|
|
|