Sinusspannung mit Offset

Rechner und Formeln zur Berechnung des Effektivwert einer Sinusspannung mit Offset

Sinus mit Offset Rechner

Sinusspannung mit Gleichspannungsoffset

Diese Funktion berechnet den Effektivwert einer Sinusspannung mit überlagerter Gleichspannung. Geben Sie die obere und untere Spitzenspannung ein.

V
V
Ergebnisse
Effektivspannung (gesamt):
Offsetspannung (DC):

Sinusspannung mit Offset

Sinusspannung mit Offset

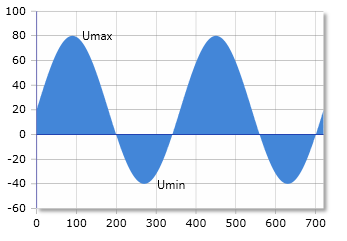
Sinusspannung mit ±60V überlagert von 20V Gleichspannung

Parameter
\(\displaystyle U_{max}\) = Obere Spitzenspannung [V]
\(\displaystyle U_{min}\) = Untere Spitzenspannung [V]
\(\displaystyle U_{eff}\) = Gesamter Effektivwert [V]
\(\displaystyle U_O\) = DC-Offset (Gleichspannung) [V]
\(\displaystyle U_s\) = AC-Spitzenspannung [V]
Grundformeln
\[U_s = \frac{U_{max} - U_{min}}{2}\]
\[U_O = \frac{U_{max} + U_{min}}{2}\]
\[U_{eff} = \sqrt{\left(\frac{U_s}{\sqrt{2}}\right)^2 + U_O^2}\]

Beispielrechnungen

Praktische Rechenbeispiele

Beispiel 1: Standard Offset-Signal

Gegeben: Umax = 80V, Umin = 40V

\[U_s = \frac{80V - 40V}{2} = 20V\]
\[U_O = \frac{80V + 40V}{2} = 60V\]
\[U_{eff} = \sqrt{\left(\frac{20V}{\sqrt{2}}\right)^2 + 60^2} = \sqrt{200 + 3600} = 61{,}64V\]
Typisches Signal mit DC-Bias
Beispiel 2: Audio mit DC-Offset

Gegeben: Umax = 7V, Umin = 3V

\[U_s = \frac{7V - 3V}{2} = 2V\]
\[U_O = \frac{7V + 3V}{2} = 5V\]
\[U_{eff} = \sqrt{\left(\frac{2V}{\sqrt{2}}\right)^2 + 5^2} = \sqrt{2 + 25} = 5{,}20V\]
Audiosignal mit Gleichspannungsanteil
Beispiel 3: Sensor-Signal

Gegeben: Umax = 4,5V, Umin = 0,5V

\[U_s = \frac{4{,}5V - 0{,}5V}{2} = 2V\]
\[U_O = \frac{4{,}5V + 0{,}5V}{2} = 2{,}5V\]
\[U_{eff} = \sqrt{\left(\frac{2V}{\sqrt{2}}\right)^2 + 2{,}5^2} = \sqrt{2 + 6{,}25} = 2{,}87V\]
Typisches Single-Supply Sensor-Signal
Komponenten-Aufschlüsselung
AC-Komponente:
Spitzenwert: Us = (Umax - Umin)/2
RMS-Wert: Us/√2
Frequenzabhängig: Ja
DC-Komponente:
Offset: UO = (Umax + Umin)/2
RMS-Beitrag: UO (konstant)
Frequenzabhängig: Nein

Formeln zur Sinusspannung mit Offset

Was ist eine Sinusspannung mit Offset?

Eine Sinusspannung mit Offset entsteht, wenn eine sinusförmige Wechselspannung von einer konstanten Gleichspannung überlagert wird. Dies ist häufig in der Elektronik zu finden, besonders bei Single-Supply-Schaltungen oder wenn Signale einen DC-Bias benötigen.

Schritt-für-Schritt Berechnung

Berechungsmethode
1. Spitze-Spitze-Spannung ermitteln:
\[U_{ss} = U_{max} - U_{min}\]
2. AC-Spitzenwert berechnen:
\[U_s = \frac{U_{ss}}{2} = \frac{U_{max} - U_{min}}{2}\]
3. DC-Offset bestimmen:
\[U_O = \frac{U_{max} + U_{min}}{2}\]
4. Gesamt-RMS berechnen:
\[U_{eff} = \sqrt{\left(\frac{U_s}{\sqrt{2}}\right)^2 + U_O^2}\]

Mathematische Herleitung

RMS-Berechnung mit Offset

Für ein Signal u(t) = Ussin(ωt) + UO:

\[U_{eff} = \sqrt{\frac{1}{T} \int_0^T [U_s\sin(\omega t) + U_O]^2 \, dt}\]
\[U_{eff} = \sqrt{\frac{1}{T} \int_0^T [U_s^2\sin^2(\omega t) + 2U_sU_O\sin(\omega t) + U_O^2] \, dt}\]
\[U_{eff} = \sqrt{\frac{U_s^2}{2} + 0 + U_O^2} = \sqrt{\left(\frac{U_s}{\sqrt{2}}\right)^2 + U_O^2}\]

Der Kreuzterm verschwindet, da das Integral über sin(ωt) über eine volle Periode null ist.

Praktische Anwendungen

Elektronik-Design
  • Single-Supply Verstärker
  • Operationsverstärker-Bias
  • ADC-Eingangssignale
  • Sensor-Konditionierung
Messtechnik
  • DC-gekoppelte Messungen
  • Oszilloskop-Triggering
  • Signalanalyse
  • Kalibriersignale
Kommunikation
  • AM-Modulation mit Träger
  • Pilot-Signale
  • Bias-Tee Anwendungen
  • DC-Restore Schaltungen

Messtechnische Überlegungen

Wichtige Messaspekte
AC-gekoppelte Messung:
Zeigt nur: AC-Komponente (Us/√2)
DC-Offset: Wird ausgeblendet
RMS-Wert: Nur AC-Anteil
Anwendung: Reine Wechselspannungsmessung
DC-gekoppelte Messung:
Zeigt: Gesamtsignal (AC + DC)
DC-Offset: Wird mitgemessen
RMS-Wert: √((Us/√2)² + UO²)
Anwendung: Vollständige Signalanalyse

Spezielle Fälle

Ohne Offset (UO = 0):
\[U_{eff} = \frac{U_s}{\sqrt{2}}\]

Reduziert sich auf normale Sinusspannung

Nur DC (Us = 0):
\[U_{eff} = U_O\]

Reine Gleichspannung

Design-Hinweise

Praktische Überlegungen
  • Verstärker-Headroom: Gesamter Spannungsbereich (Umax bis Umin) berücksichtigen
  • Kopplung: AC-Kopplung entfernt DC-Offset, DC-Kopplung erhält ihn
  • Leistungsberechnung: Gesamt-RMS für thermische Verluste verwenden
  • ADC-Aussteuerung: Beiden Spitzenwerte innerhalb des Messbereichs halten
  • Filterdesign: DC-Blocker für Offset-Entfernung, Bias-Tee für Offset-Hinzufügung
  • Sicherheit: Maximale Spannung für Isolationsauslegung verwenden

Wechselstrom Funktionen

Kenngrößen der Wechselspannung • Frequenz und Periodendauer • Frequenz und Wellenlänge • Spannungswert zu einem Winkel • Spannungswert an einem Zeitpunkt • Effektivwert einer Sinusschwingung • Effektivwert einer Sinusschwingung mit Offset • Effektivwert eines Sinusimpuls (Einweg) • Effektivwert eines Sinusimpuls (Zweiweg) • Effektivwert einer Rechteckspannung • Effektivwert eines Rechteckimpuls • Effektivwert einer Dreieckspannung • Effektivwert eines Dreieckimpuls • Effektivwert Sägezahnspannung • Effektivwert eines Sägezahnimpuls