Sinusimpuls Effektivspannung (Zweiweggleichrichtung)

Rechner und Formeln zur Berechnung des Effektiv- und Mittelwerts von Sinusimpulsen

Sinusimpuls Rechner (Zweiweg)

Zweiweggleichrichtung

Diese Funktion berechnet den Effektivwert und den Mittelwert eines Sinusimpuls aus einer Zweiweggleichrichtung. Beide Halbwellen werden gleichgerichtet.

V
Ergebnisse
Effektivspannung:
Mittelspannung:

Zweiweggleichrichtung

Sinusimpuls nach einer Zweiweggleichrichtung

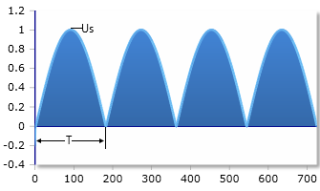
Sinusimpuls nach einer Zweiweggleichrichtung - beide Halbwellen gleichgerichtet

Parameter
\(\displaystyle U_s\) = Spitzenspannung [V]
\(\displaystyle U_{eff}\) = Effektivspannung [V]
\(\displaystyle U_m\) = Mittelspannung [V]
Grundformeln
\[U_{eff} = \frac{U_s}{\sqrt{2}}\]
\[U_m = \frac{2 \cdot U_s}{\pi}\]

Beispielrechnungen

Praktische Rechenbeispiele

Beispiel 1: Standard Zweiweggleichrichtung

Gegeben: Us = 10V (Spitzenspannung der Sinuswelle)

\[U_{eff} = \frac{10V}{\sqrt{2}} = \frac{10V}{1{,}414} = 7{,}07V\]
\[U_m = \frac{2 \cdot 10V}{\pi} = \frac{20V}{3{,}14159} = 6{,}37V\]
Optimale Energieausnutzung mit 70,7% Effektivwert
Beispiel 2: Netzspannung zweiweggleichgerichtet

Gegeben: Us = 325V (Spitze der 230V Netzspannung)

\[U_{eff} = \frac{325V}{\sqrt{2}} = 230V\]
\[U_m = \frac{2 \cdot 325V}{\pi} = 207V\]
Vollständige Ausnutzung der Netzspannung
Beispiel 3: Niederspannungsnetzteil

Gegeben: Us = 17V (12V Trafo mit √2-Faktor)

\[U_{eff} = \frac{17V}{\sqrt{2}} = 12{,}0V\]
\[U_m = \frac{2 \cdot 17V}{\pi} = 10{,}8V\]
Typisches 12V-Netzteil nach Gleichrichtung
Verhältnisse bei Zweiweggleichrichtung
Effektivwert-Verhältnis:
Ueff / Us: 1/√2 ≈ 0,707
Prozentual: ≈ 70,7%
Faktor: 0,707
Mittelwert-Verhältnis:
Um / Us: 2/π ≈ 0,637
Prozentual: ≈ 63,7%
Faktor: 0,637

Theorie der Zweiweggleichrichtung

Was ist eine Zweiweggleichrichtung?

Bei einer Zweiweggleichrichtung wird sowohl der positive als auch der negative Teil der sinusförmigen Wechselspannung genutzt, sodass die gesamte Welle in positive Spannungen umgewandelt wird. Dies führt zu einer deutlich besseren Energieausnutzung im Vergleich zur Einweggleichrichtung.

Effektivwert nach Zweiweggleichrichtung

Der Effektivwert ist definiert als Gleichstromwert mit der gleichen Wärmewirkung wie der betrachtete Wechselstrom. Die Effektivspannung (RMS-Spannung) nach einer Zweiweggleichrichtung ergibt sich als Quadratwurzel des mittleren quadratischen Werts über die gesamte Periode. Da beide Halbwellen genutzt werden, bleibt der Effektivwert gleich dem der ursprünglichen Sinusspannung.

Effektivwert-Formel
\[U_{eff} = \frac{U_s}{\sqrt{2}}\]

Der Effektivwert entspricht dem einer normalen Sinusspannung (≈ 70,7%).

Mittelwert nach Zweiweggleichrichtung

Die Mittelspannung (Durchschnittsspannung) nach einer Zweiweggleichrichtung berechnet sich aus dem Mittelwert der gesamten positiven und negativen Halbwellen. Da beide Halbwellen gleichgerichtet werden, ist der Mittelwert doppelt so hoch wie bei der Einweggleichrichtung.

Mittelwert-Formel
\[U_m = \frac{2 \cdot U_s}{\pi}\]

Der Mittelwert beträgt etwa 63,7% der Spitzenspannung.

Mathematische Herleitung

Berechnung des Effektivwerts

Für einen zweiweggleichgerichteten Sinus über eine volle Periode T:

\[U_{eff} = \sqrt{\frac{1}{T} \int_0^T u^2(t) \, dt}\]
Für 0 ≤ t ≤ T/2: u(t) = Us sin(ωt) (positive Halbwelle)
Für T/2 < t ≤ T: u(t) = Us |sin(ωt)| (negative Halbwelle gleichgerichtet)
\[U_{eff} = \sqrt{\frac{1}{T} \int_0^T U_s^2 \sin^2(\omega t) \, dt} = \frac{U_s}{\sqrt{2}}\]
Berechnung des Mittelwerts

Der Mittelwert wird über eine volle Periode berechnet:

\[U_m = \frac{1}{T} \int_0^T |u(t)| \, dt\]
\[U_m = \frac{2}{T} \int_0^{T/2} U_s \sin(\omega t) \, dt = \frac{2 \cdot U_s}{\pi}\]

Praktische Anwendungen

Netzteile
  • Standard-Gleichrichter
  • Hohe Effizienz
  • Niedrige Brummspannung
  • Gute Transformator-Ausnutzung
Industrielle Anwendungen
  • DC-Motorantriebe
  • Batterieladegeräte
  • Galvanik-Anlagen
  • Schweißgeräte
Elektronik
  • Verstärker-Netzteile
  • LED-Treiber
  • Spannungsregler-Eingänge
  • Labor-Netzgeräte

Vergleich der Gleichrichtungsarten

Gleichrichtungsvergleich
Keine Gleichrichtung:
Ueff = Us/√2 ≈ 0,707
Um = 0V
Wechselstrom
Einweggleichrichtung:
Ueff = Us/2 = 0,5
Um = Us/π ≈ 0,318
50% Effizienz
Zweiweggleichrichtung:
Ueff = Us/√2 ≈ 0,707
Um = 2Us/π ≈ 0,637
100% Effizienz

Vorteile der Zweiweggleichrichtung

Elektrische Vorteile:
  • Doppelte Effizienz: 100% vs. 50% bei Einweg
  • Niedriger Brumm: 100Hz vs. 50Hz Grundfrequenz
  • Bessere Ausnutzung: Transformator und Dioden
  • Höhere Spannung: Doppelter Mittelwert
Praktische Vorteile:
  • Kleinere Filter: Weniger Kondensatorkapazität
  • Bessere Regelung: Gleichmäßigere DC-Spannung
  • Weniger Erwärmung: Geringere Verluste
  • Standard-Lösung: In den meisten Netzteilen

Design-Hinweise

Praktische Überlegungen
  • Schaltungsarten: Brückengleichrichter oder Mittelpunktschaltung
  • Dioden-Spannungsfestigkeit: Mindestens 1,4 × Us (Brücke) oder 2,8 × Us (Mittelpunkt)
  • Strombelastung: Gleichmäßigere Verteilung auf die Dioden
  • Transformator-Design: Bessere Ausnutzung des Eisenkerns
  • Filterauslegung: Kondensator für 100Hz (bzw. 2 × fNetz) dimensionieren
  • Kosteneffizienz: Höhere Anfangsinvestition, aber bessere Gesamteffizienz

Wechselstrom Funktionen

Kenngrößen der Wechselspannung • Frequenz und Periodendauer • Frequenz und Wellenlänge • Spannungswert zu einem Winkel • Spannungswert an einem Zeitpunkt • Effektivwert einer Sinusschwingung • Effektivwert einer Sinusschwingung mit Offset • Effektivwert eines Sinusimpuls (Einweg) • Effektivwert eines Sinusimpuls (Zweiweg) • Effektivwert einer Rechteckspannung • Effektivwert eines Rechteckimpuls • Effektivwert einer Dreieckspannung • Effektivwert eines Dreieckimpuls • Effektivwert Sägezahnspannung • Effektivwert eines Sägezahnimpuls