Frequenz und Wellenlängen

Rechner und Formeln zur Berechnung von Frequenz und Wellenlänge

Frequenz / Wellenlänge Rechner

Frequenz-Wellenlängen-Rechner

Auf dieser Seite können Sie die Wellenlängen zu einer bestimmten Frequenz, oder die Frequenz zu einer Wellenlänge berechnen. Es können Wellenlängen für elektrische Schwingungen, Licht und Schall berechnet werden.

Was soll berechnet werden?
Ergebnis
Wellenlänge:
Frequenz:

Frequenz & Wellenlänge

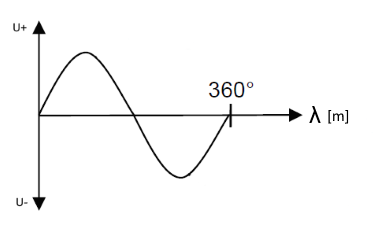
Eine Periode einer Sinusschwingung

Wellenlänge λ einer periodischen Schwingung

Parameter
\(\displaystyle \lambda\) = Wellenlänge [m]
\(\displaystyle f\) = Frequenz [Hz]
\(\displaystyle c\) = Ausbreitungsgeschwindigkeit [m/s]
Grundformeln
\[\lambda = \frac{c}{f}\]
\[f = \frac{c}{\lambda}\]
Tipp

Einen Rechner zur Berechnung von Frequenz und Periodendauer finden Sie hier.

Ausbreitungsgeschwindigkeiten

Geschwindigkeiten verschiedener Wellenarten

Die Wellenlänge ist abhängig von der Frequenz und der Ausbreitungsgeschwindigkeit der Wellen. Die folgende Tabelle zeigt die Ausbreitungsgeschwindigkeit verschiedener Wellen in unterschiedlichen Medien.

Elektromagnetische Wellen
Freier Raum (Vakuum):
299.792.458 km/s
Elektrische Leitungen:
≈ 240.000 km/s
Kupfer-Leiterplatten:
≈ 200.000 km/s
Lichtwellen:
299.792.458 km/s
Mechanische Wellen
Schall in Luft (+20°C):
343 m/s
Schall in Wasser:
1.470 m/s
Schall in Stahl:
≈ 5.000 m/s
Seismische Wellen:
1-14 km/s

Beispielrechnungen

Praktische Rechenbeispiele

Beispiel 1: Berechnung der Frequenz

Gegeben: λ = 10m, c = 300 m/s (beispielhafte Schallgeschwindigkeit)

\[f = \frac{c}{\lambda} = \frac{300 \text{ m/s}}{10 \text{ m}} = 30 \text{ Hz}\]
Niederfrequente Schallwelle
Beispiel 2: Berechnung der Wellenlänge

Gegeben: f = 50Hz, c = 340 m/s (Schallgeschwindigkeit in Luft)

\[\lambda = \frac{c}{f} = \frac{340 \text{ m/s}}{50 \text{ Hz}} = 6{,}8 \text{ m}\]
Tieffrequente Schallwelle in Luft
Beispiel 3: Elektromagnetische Welle

Gegeben: f = 100MHz (UKW-Radio), c = 3×10⁸ m/s

\[\lambda = \frac{3 \times 10^8 \text{ m/s}}{100 \times 10^6 \text{ Hz}} = 3 \text{ m}\]
UKW-Radiofrequenz mit 3m Wellenlänge
Wellenlängen-Spektrum
Radiowellen:
Langwelle: 1-10 km
Mittelwelle: 100-1000 m
Kurzwelle: 10-100 m
UKW: 1-10 m
Mikrowellen:
WLAN 2,4GHz: 12,5 cm
WLAN 5GHz: 6 cm
Radar: 1-30 cm
Mikrowelle: 12,2 cm
Licht:
Infrarot: 0,7-1000 µm
Sichtbar: 380-780 nm
Ultraviolett: 10-380 nm
Röntgen: 0,01-10 nm

Formeln zur Frequenz und Wellenlänge

Grundlagen der Wellenausbreitung

Die Wellenlänge bezeichnet die Länge einer Periode einer sich ausbreitenden Schwingung. Sie ist abhängig von der Frequenz und der Ausbreitungsgeschwindigkeit der Wellen.

Grundlegende Beziehungen

Die Wellenlänge λ in Meter berechnet sich, indem man die Ausbreitungsgeschwindigkeit c durch die Frequenz f teilt.

Wellenlängen-Formel
\[\lambda = \frac{c}{f}\]

Die Wellenlänge ist proportional zur Geschwindigkeit und umgekehrt proportional zur Frequenz.

Daraus ergibt sich zur Berechnung der Frequenz die folgende Formel:

Frequenz-Formel
\[f = \frac{c}{\lambda}\]

Die Frequenz ist proportional zur Geschwindigkeit und umgekehrt proportional zur Wellenlänge.

Verschiedene Wellentypen

Elektromagnetische Wellen
  • Ausbreitung: Im Vakuum mit Lichtgeschwindigkeit
  • Medium: Benötigen kein Übertragungsmedium
  • Geschwindigkeit: c = 299.792.458 m/s
  • Spektrum: Radio bis Gammastrahlung
Mechanische Wellen
  • Ausbreitung: Benötigen ein Medium
  • Medium: Luft, Wasser, Festkörper
  • Geschwindigkeit: Materialabhängig
  • Beispiele: Schall, Seismik, Wasserwellen

Praktische Anwendungen

Funktechnik
  • Antennendesign
  • Frequenzbänder
  • Ausbreitungsmodelle
  • Interferenz-Analyse
Optik
  • Farbspektrum
  • Beugungsgitter
  • Lasertechnik
  • Spektroskopie
Akustik
  • Raumakustik
  • Ultraschall
  • Musikinstrumente
  • Lärmschutz

Legende

Symbol-Definitionen
λ (Lambda): Wellenlänge in Meter [m]
f: Frequenz in Hertz [Hz]
c: Ausbreitungsgeschwindigkeit [m/s]
T: Periodendauer in Sekunden [s]
ω: Kreisfrequenz [rad/s]
k: Wellenzahl [1/m]

Design-Hinweise

Praktische Überlegungen
  • Antennendesign: Optimale Länge bei λ/4, λ/2 oder Vielfachen
  • Wellenausbreitung: Hindernisse können bei λ-Größe Beugung verursachen
  • Interferenz: Konstruktive/destruktive Überlagerung bei λ/2-Abständen
  • Resonanz: Hohlraumresonatoren bei λ/2-Abmessungen
  • Dispersion: Geschwindigkeit kann frequenzabhängig sein
  • Dämpfung: Verluste oft frequenz- und mediumsabhängig

Wechselstrom Funktionen

Kenngrößen der Wechselspannung • Frequenz und Periodendauer • Frequenz und Wellenlänge • Spannungswert zu einem Winkel • Spannungswert an einem Zeitpunkt • Effektivwert einer Sinusschwingung • Effektivwert einer Sinusschwingung mit Offset • Effektivwert eines Sinusimpuls (Einweg) • Effektivwert eines Sinusimpuls (Zweiweg) • Effektivwert einer Rechteckspannung • Effektivwert eines Rechteckimpuls • Effektivwert einer Dreieckspannung • Effektivwert eines Dreieckimpuls • Effektivwert Sägezahnspannung • Effektivwert eines Sägezahnimpuls