Effektivwert eines Dreieckimpuls
Rechner und Formeln zur Berechnung des Effektiv- und Mittelwerts eines Dreieckimpulses
Dreieckimpuls Rechner
Dreieckimpuls
Diese Funktion berechnet den Effektivwert und den Mittelwert eines Dreieckimpulses. Zur Berechnung wird der Wert der Spitzenspannung eingegeben.
Dreieckimpuls & Parameter
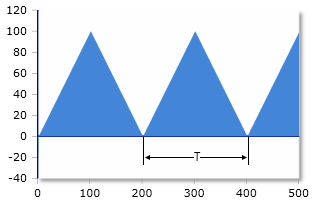
Parameter
Grundformeln
|
|
Beispielrechnungen
Praktische Rechenbeispiele
Beispiel 1: Standard Dreieckimpuls
Gegeben: Us = 10V
Beispiel 2: Audio-Anwendung
Gegeben: Us = 3V (typischer Audio-Pegel)
Beispiel 3: Hochspannung
Gegeben: Us = 100V
Verhältnisse beim Dreieckimpuls
Effektivwert-Verhältnis:
Mittelwert-Verhältnis:
Formel zum Dreieckimpuls
Was ist ein Dreieckimpuls?
Der Effektivwert eines Dreieckimpulses (der meist als Dreieckspannung mit periodischen Impulsen bezeichnet wird) kann auf ähnliche Weise berechnet werden wie der Effektivwert einer klassischen Dreieckwelle. Wichtig dabei ist, dass die Dreieckspannung eine symmetrische Form hat, bei der die Spannung zwischen positiven und negativen Spitzenwerten wechselt.
Definition des Effektivwerts
Der Effektivwert ist definiert als Gleichstromwert mit der gleichen Wärmewirkung wie der betrachtete Wechselstrom. Er errechnet sich für Dreieckimpulse nach der folgenden Formel:
Effektivwert
Der Effektivwert beträgt etwa 57,7% der Spitzenspannung.
Mittelwert
Der Mittelwert beträgt 50% der Spitzenspannung.
Mathematische Herleitung
Berechnung
Für einen symmetrischen Dreieckimpuls mit der Periode T und Spitzenspannung Us:
Praktische Anwendungen
Signalerzeugung
- Funktionsgeneratoren
- Modulationsverfahren
- Testsignale
- Wobbelgeneratoren
Messtechnik
- Oszilloskope
- Spektrumanalysatoren
- Effektivwertmessung
- Kalibrierung
Leistungselektronik
- PWM-Signale
- Dreiecksvergleicher
- Schaltregler
- Motorsteuerung
Vergleich mit anderen Signalformen
Effektivwert-Faktoren
Ueff = Us/√2 ≈ 0,707
Ueff = Us/√3 ≈ 0,577
Ueff = Us = 1,0
Ueff = Us/√3 ≈ 0,577
|
|