Deltoidal Hexecontahedron Calculator
Calculator and formulas for calculating a deltoidal hexecontahedron
Deltoidal Hexecontahedron Calculator
The Deltoidal Hexecontahedron
A Deltoidal Hexecontahedron is a Catalan solid with 60 kite-shaped deltoidal faces.
Deltoidal Hexecontahedron Properties
The Kite Body: Dual to the rhombicosidodecahedron
Deltoidal Hexecontahedron Structure
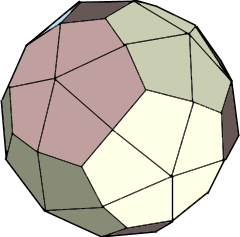
The fascinating kite-shaped body with 60 deltoidal faces.
Dual to the rhombicosidodecahedron.
|
|
What is a Deltoidal Hexecontahedron?
A Deltoidal Hexecontahedron is a fascinating Catalan solid:
- Definition: Polyhedron with 60 deltoidal faces (kite quadrilaterals)
- Faces: Each face is a convex quadrilateral (deltoid)
- Dual: To the rhombicosidodecahedron (Archimedean solid)
- Vertices: 62 identical vertices
- Edges: 120 edges in two lengths
- Symmetry: Icosahedral symmetry group
Geometric Properties of the Deltoidal Hexecontahedron
The Deltoidal Hexecontahedron exhibits remarkable geometric properties:
Basic Parameters
- Edge Lengths: Two different edge lengths a and b
- Faces: 60 congruent deltoidal faces
- Euler Characteristic: V - E + F = 62 - 120 + 60 = 2
- Dual Form: Rhombicosidodecahedron
Special Properties
- Catalan Solid: Dual to Archimedean solid
- Deltoidal Faces: Each face is a kite quadrilateral
- Golden Ratio: Proportions contain φ
- Icosahedral Symmetry: 120 symmetry operations
Mathematical Relationships
The Deltoidal Hexecontahedron follows complex mathematical laws involving the golden ratio:
Volume Formula
Complex formula with nested radicals. Coefficient ≈ 22.21 from icosahedral geometry.
Surface Area Formula
Sum of 60 deltoidal faces. Golden ratio √5 in complex form.
Applications of the Deltoidal Hexecontahedron
Deltoidal Hexecontahedra find applications in specialized fields:
Science & Research
- Crystallography and mineral structure analysis
- Complex molecular cage structures
- Mathematical topology studies
- Symmetry group theory
Technology & Design
- 3D modeling and computer graphics
- Algorithm testing for complex geometries
- Architectural design elements
- Mathematical visualization tools
Education & Teaching
- Geometry instruction and demonstrations
- Catalan solid studies
- Duality principles in mathematics
- Symmetry and group theory
Art & Design
- Sculptural installations
- Mathematical art and design
- Decorative patterns and motifs
- Architectural ornaments
Formulas for the Deltoidal Hexecontahedron
Surface Area A
Surface area with golden ratio √5
Volume V
Volume with complex nested radicals
Circumradius RK
Circumradius with golden ratio
Inradius RI
Inradius with √5-dependency
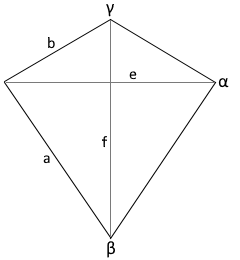
Deltoid Properties
Base parameter
b ≈ a/1.54
e ≈ 1.115·a
f ≈ 1.163·a
Each of the 60 deltoidal faces has these properties
Angles in the Deltoid
≈ 86° 58' 27"
≈ 67° 46' 59"
≈ 118° 16' 7"
The characteristic angles of each deltoidal face
Calculation Example for a Deltoidal Hexecontahedron
Given
Find: All properties of the kite-shaped body
1. Surface Area Calculation
The surface area is approximately 156 square units
2. Volume Calculation
The volume is approximately 178 cubic units
3. Circumradius
The circumradius is approximately 3.51 units
4. Inradius
The inradius is approximately 3.42 units
5. Deltoid Properties
The fascinating kite-shaped body with complex mathematical beauty
The Deltoidal Hexecontahedron: The Mysterious Kite-Shaped Body
The Deltoidal Hexecontahedron is one of the most fascinating and mysterious among the Catalan solids. With its 60 kite-shaped deltoidal faces, it embodies a unique connection between mathematical complexity and geometric elegance. As the dual solid to the rhombicosidodecahedron, it represents the deepest secrets of icosahedral symmetry and the golden ratio, where each of its 60 identical faces forms a perfect kite quadrilateral connected to all other faces through complex mathematical relationships.
The Geometry of Deltoidal Faces
The Deltoidal Hexecontahedron fascinates through its unique face properties:
- 60 Deltoidal Faces: Each face is a convex kite quadrilateral with two pairs of equal sides
- Two Edge Lengths: Each deltoid has a long edge (a) and a short edge (b)
- Characteristic Angles: Side angle ≈ 87°, base angle ≈ 68°, apex angle ≈ 118°
- Symmetry Axes: Each deltoid has one axis of symmetry through vertices of different angles
- Golden Ratio: All proportions are based on the golden ratio φ = (1+√5)/2
- Perfect Arrangement: The 60 deltoids fit together to form a completely symmetrical body
- Duality Principle: Each deltoidal face corresponds to a vertex of the dual rhombicosidodecahedron
Catalan Solids and Duality
Catalan Tradition
Named after Eugène Charles Catalan (1814-1894), this polyhedron belongs to the 13 Catalan solids - the dual forms of the Archimedean solids. It shows how uniform vertices can create congruent faces.
Duality Principle
As the dual to the rhombicosidodecahedron (with 62 vertices, 120 edges, 60 faces), it systematically exchanges vertices and faces: 60 faces become 60 vertices, while the edge count remains the same.
Icosahedral Symmetry
With full icosahedral symmetry group (120 symmetry operations), it belongs to the most symmetrical three-dimensional forms ever, explaining its fascinating geometric perfection.
Mathematical Complexity
The formulas contain multiple nested radical expressions with the golden ratio, showing the deep connection to pentagonal geometry and the Fibonacci sequence.
The Golden Ratio in Deltoid Geometry
The Deltoidal Hexecontahedron is permeated by the golden ratio:
Proportional Relationships
The ratio of long to short edge is approximately 1.54, closely related to the golden ratio φ ≈ 1.618. This proportion creates the harmonic appearance of the deltoidal faces.
Formula Structures
Virtually all geometric formulas contain √5 terms directly related to the golden ratio: φ = (1+√5)/2. This shows the fundamental role of pentagonal geometry.
Angular Relationships
The characteristic angles of the deltoidal faces arise from constructions based on the golden ratio, belonging to the most harmonious proportions in geometry.
Symmetric Perfection
The 60-fold repetition of identical deltoidal faces in perfect icosahedral arrangement shows how the golden ratio can create three-dimensional harmony.
Scientific and Cultural Significance
The Deltoidal Hexecontahedron finds applications in various fields:
- Crystallography: Model for complex crystal structures with icosahedral symmetry
- Molecular Chemistry: Template for large molecular cages and fullerene derivatives
- Mathematical Research: Study object for symmetry groups and topology
- Geometric Art: Inspiration for sculptural works and architecture
- Education: Demonstration of duality principles and symmetry concepts
- Computer Graphics: Benchmark for complex 3D modeling algorithms
- Philosophy: Symbol of harmony between complexity and order
Construction and Mathematical Challenges
Construction Difficulties
Manufacturing a perfect Deltoidal Hexecontahedron requires highest precision in creating the 60 deltoidal faces. Each face must have exact angles and edge lengths defined by irrational numbers.
Mathematical Complexity
The calculations require multiple nested radical expressions and transcendental functions, making this body one of the most computationally demanding geometric objects.
Modern Technology
Only with modern CAD software and precision manufacturing has it become possible to create physical models with the required accuracy to realize theoretical perfection.
Quality Control
Verification of geometric correctness requires high-precision measurement methods and computer-aided analysis systems, as even smallest deviations can destroy symmetry.
Philosophical and Aesthetic Dimensions
Harmony of Opposites
The Deltoidal Hexecontahedron embodies the harmony between simplicity (identical deltoidal faces) and complexity (60-fold arrangement in icosahedral symmetry), making it a philosophical symbol.
Natural Beauty
The proportions based on the golden ratio give this body a natural beauty that is both mathematically founded and aesthetically appealing.
Educational Value
As a demonstration object for duality, symmetry, and complex geometric relationships, it offers unparalleled opportunities for mathematics education and science communication.
Cultural Symbolism
In various cultures, kite-shaped structures are associated with harmony, balance, and spiritual completion, giving this body additional symbolic meaning.
Summary
The Deltoidal Hexecontahedron stands as one of the most mysterious and mathematically demanding Catalan solids. Its 60 kite-shaped deltoidal faces, permeated by the golden ratio and arranged in perfect icosahedral symmetry, make it a masterpiece of geometry. From its discovery as the dual solid to the rhombicosidodecahedron to its modern applications in science and art, it shows how mathematical complexity and aesthetic beauty can form an inseparable unity. As a bridge between the ancient tradition of Platonic solids and the modern challenges of computational geometry, it remains a fascinating subject for researchers, artists, and all who are inspired by the power of mathematics to create perfect forms.