Deltoidal Icositetrahedron Calculator
Calculator and formulas for calculating a deltoidal icositetrahedron
Deltoidal Icositetrahedron Calculator
The Deltoidal Icositetrahedron
A Deltoidal Icositetrahedron is a Catalan solid with 24 kite-shaped deltoidal faces and cubic symmetry.
Deltoidal Icositetrahedron Properties
The Compact Kite Body: Dual to the rhombicuboctahedron
Deltoidal Icositetrahedron Structure
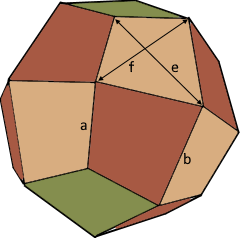
The compact kite-shaped body with 24 deltoidal faces.
Cubic symmetry with perfect harmony.
|
|
What is a Deltoidal Icositetrahedron?
A Deltoidal Icositetrahedron is a compact Catalan solid with cubic symmetry:
- Definition: Polyhedron with 24 deltoidal faces (kite quadrilaterals)
- Faces: Each face is a convex kite quadrilateral
- Dual: To the rhombicuboctahedron
- Vertices: 26 vertices (8 threefold + 18 fourfold)
- Edges: 48 edges in two lengths
- Symmetry: Cubic symmetry group
Geometric Properties of the Deltoidal Icositetrahedron
The Deltoidal Icositetrahedron exhibits fascinating cubic properties:
Basic Parameters
- Edge Lengths: Two different edge lengths a and b
- Faces: 24 congruent deltoidal faces
- Euler Characteristic: V - E + F = 26 - 48 + 24 = 2
- Dual Form: Rhombicuboctahedron
Cubic Properties
- Catalan Solid: Dual to uniform polyhedron
- Deltoidal Faces: Each face is a kite quadrilateral
- Square Root 2 Geometry: Proportions contain √2
- Cubic Symmetry: 48 symmetry operations
Mathematical Relationships
The Deltoidal Icositetrahedron follows cubic mathematical laws with √2:
Volume Formula
Cubic formula with √2 terms. Coefficient ≈ 6.90 from cubic geometry.
Surface Area Formula
Sum of 24 deltoidal faces. Square root 2 geometry in compact form.
Applications of the Deltoidal Icositetrahedron
Deltoidal Icositetrahedra find applications in cubic structures:
Cubic Structures
- Crystallography of cubic systems
- Architectural modular elements
- Compact space filling and tessellation
- Metallic lattice structures
Engineering
- Mechanical components with cubic symmetry
- 3D printer calibration objects
- Precision measuring tools
- Robotics and automation
Mathematical Education
- Cubic symmetry demonstrations
- Catalan solid studies
- Duality principles in geometry
- √2 geometry and root relationships
Design & Art
- Cubic sculptures and installations
- Geometric patterns and ornaments
- Modular design elements
- Architectural facade design
Formulas for the Deltoidal Icositetrahedron
Surface Area A
Surface area with √2 terms from cubic geometry
Volume V
Volume with cubic √2 relationships
Circumradius RK
Simple cubic formula with √2
Inradius RI
Inradius with √2 dependency
Deltoid Properties (Cubic Version)
Base parameter
b = a(4+√2)/7
e ≈ 1.17·a
f ≈ 1.31·a
Each of the 24 deltoidal faces has cubic √2 proportions
Cubic Edge Ratios
a/b = 7/(4+√2) ≈ 1.29
Square root 2 dominates all proportions
Characteristic √2 relationships of cubic symmetry
Calculation Example for a Deltoidal Icositetrahedron
Given
Find: All properties of the compact kite-shaped body
1. Surface Area Calculation
The surface area is approximately 165 square units
2. Volume Calculation
The volume is approximately 186 cubic units
3. Circumradius
The circumradius is approximately 3.62 units
4. Short Edge
The short edge is approximately 2.32 units
5. The Cubic Kite-Shaped Body
The compact kite-shaped body with perfect cubic harmony
The Deltoidal Icositetrahedron: The Cubic Kite-Shaped Body
The Deltoidal Icositetrahedron is a fascinating Catalan solid that combines the elegance of cubic symmetry with the complex beauty of deltoidal faces. With its 24 kite-shaped faces arranged in perfect cubic harmony, it represents a remarkable synthesis of geometric compactness and mathematical sophistication. As the dual solid to the rhombicuboctahedron, it embodies the deepest principles of cubic geometry, where the characteristic square-root-2 mathematics permeates all its proportions and relationships, giving it a unique position among the Catalan solids.
The Cubic Harmony of Deltoidal Faces
The Deltoidal Icositetrahedron fascinates through its cubic perfection:
- 24 Deltoidal Faces: Each face is a convex kite quadrilateral with cubic proportions
- Cubic Symmetry: Octahedral symmetry group with 48 symmetry operations
- Two Edge Lengths: Long edge (a) and short edge (b) in √2 ratio
- Compact Structure: 26 vertices (8 threefold, 18 fourfold) in optimal arrangement
- Square Root 2 Geometry: All proportions based on √2 ≈ 1.414
- Perfect Tessellation: The 24 deltoids fit together seamlessly
- Duality Principle: Each deltoidal face corresponds to a vertex of the dual polyhedron
Catalan Tradition and Cubic Duality
Catalan Elegance
As one of the 13 Catalan solids, the Deltoidal Icositetrahedron shows how uniform vertices can create congruent faces. The cubic symmetry makes it a particularly elegant representative of this family.
Cubic Duality
As the dual to the rhombicuboctahedron, it systematically exchanges vertices and faces, while the cubic structure is preserved and the √2 relationships are reinforced.
Compact Perfection
With only 24 faces, it achieves remarkable structural compactness, making it an ideal demonstration object for cubic symmetry and deltoid geometry.
Mathematical Clarity
The formulas are relatively simple and elegant due to the cubic structure, with clear √2 relationships that facilitate understanding of the underlying geometry.
The Square Root 2 Geometry of Cubic Order
The Deltoidal Icositetrahedron is permeated by √2 relationships:
Cubic Proportions
The ratio of long to short edge follows the cubic relationship a/b = 7/(4+√2) ≈ 1.29, which emerges directly from the octahedral symmetry of the underlying cube.
Square Root 2 Formulas
Virtually all geometric formulas contain √2 terms that reflect the fundamental cubic nature of this polyhedron and distinguish it from the φ-based icosahedral solids.
Cubic Harmony
The arrangement of the 24 deltoidal faces follows the laws of cubic symmetry, whereby each face stands in perfect harmony with all others, creating a remarkable structural unity.
Geometric Efficiency
The cubic organization enables exceptionally efficient space utilization while maintaining the characteristic deltoid properties of each individual face.
Scientific and Technical Significance
The Deltoidal Icositetrahedron finds diverse applications:
- Cubic Crystallography: Model for complex cubic crystal structures
- Precision Technology: Reference object for cubic symmetry measurements
- Architecture: Modular building elements with cubic symmetry
- Mechanics: Compact mechanical components with deltoid surfaces
- Education: Ideal teaching object for cubic geometry and duality
- 3D Printing: Calibration object for precision 3D printers
- Materials Science: Template for cubic lattice structures
Construction and Cubic Precision
Cubic Precision
Manufacturing requires highest precision in maintaining cubic symmetry. Each of the 24 deltoidal faces must exhibit exact √2 proportions to ensure overall symmetry.
Manufacturing Advantages
The cubic structure facilitates manufacturing because the basic orientations correspond to standard coordinate axes, allowing optimal use of conventional manufacturing processes.
Quality Control
Verification of cubic symmetry can be performed with standard measuring instruments, simplifying quality assurance and enabling cost-effective production.
Modern Manufacturing
CNC machines and 3D printers can precisely implement cubic relationships, making high-quality physical models realizable for research and education.
Aesthetic and Educational Dimensions
Cubic Aesthetics
The combination of cubic order and deltoid elegance creates a unique aesthetic effect that radiates both mathematical rationality and organic beauty.
Educational Value
As a compact example of Catalan solids with cubic symmetry, it is ideally suited to teach students the principles of duality and √2 geometry.
Symbolic Meaning
In design philosophy, it symbolizes the perfect balance between structural efficiency and aesthetic sophistication, between mathematical order and natural elegance.
Cultural Relevance
As a representative of the cubic family of geometric forms, it connects with cultural traditions that value order, stability, and craftsmanship precision.
Summary
The Deltoidal Icositetrahedron embodies the perfect synthesis of cubic order and deltoid elegance. With its 24 kite-shaped faces arranged in perfect octahedral symmetry, it shows how mathematical principles can create geometric beauty of remarkable compactness and clarity. The consistent √2 relationships connect it deeply with cubic geometry and make it an ideal study object for exploring duality, symmetry, and the fundamental principles of three-dimensional geometry. From its theoretical significance in pure mathematics to its practical applications in technology and design, the Deltoidal Icositetrahedron remains a fascinating example of how elegant mathematical structures can provide both intellectual satisfaction and practical utility.