Tetrakis Hexahedron Calculator
Calculator and formulas for calculating a tetrakis hexahedron
Tetrakis Hexahedron Calculator
The Tetrakis Hexahedron
A Tetrakis Hexahedron is a Catalan solid with 24 isosceles triangular faces - dual to the truncated octahedron.
Tetrakis Hexahedron Properties
The Cubic Pyramid Master: Dual to the truncated octahedron
Tetrakis Hexahedron Structure
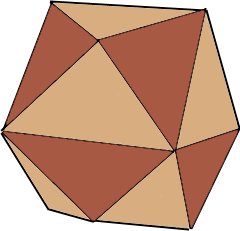
The cubic pyramid master with 24 triangular faces.
Dual to the truncated octahedron.
|
|
What is a Tetrakis Hexahedron?
A Tetrakis Hexahedron is a fundamental Catalan solid with cubic foundation:
- Definition: Polyhedron with 24 isosceles triangular faces
- Faces: Each face is an isosceles triangle
- Dual: To the truncated octahedron
- Vertices: 14 vertices with different coordination
- Edges: 36 edges in two types
- Structure: Cube with pyramids on each face
Geometric Properties of the Tetrakis Hexahedron
The Tetrakis Hexahedron exhibits cubic-pyramid geometric properties:
Cubic Foundation
- Base Structure: Central cube with edge length a
- Pyramid Addition: 6 pyramids on cube faces
- Euler Characteristic: V - E + F = 14 - 36 + 24 = 2
- Dual Form: Truncated octahedron
Pyramid Properties
- Catalan Solid: Dual to Archimedean solid
- Triangular Faces: Each face is an isosceles triangle
- Simple Mathematics: Basic fractional relationships
- Construction: Cube + 6 identical pyramids
Mathematical Relationships
The Tetrakis Hexahedron follows simple mathematical laws:
Volume Formula
Simple fractional formula. Clean geometric relationship.
Surface Area Formula
Sum of 24 isosceles triangles. Simple √5 factor.
Applications of the Tetrakis Hexahedron
Tetrakis Hexahedra find applications in cubic-based structures:
Scientific Research
- Cubic crystal studies
- Pyramid-based structures
- Materials science applications
- Geometric modeling
Engineering
- Structural design applications
- Cubic-pyramid combinations
- Architectural elements
- Manufacturing templates
Education
- Basic geometry education
- Cubic structure studies
- Catalan solid introduction
- 3D modeling tutorials
Art & Design
- Cubic-pyramid sculptures
- Architectural ornaments
- Geometric art projects
- 3D printing models
Formulas for the Tetrakis Hexahedron
Pyramid Edge (b)
Pyramid edge in terms of cube edge
Height (h)
Total height of the polyhedron
Surface Area (A)
Surface area with √5 factor
Volume (V)
Simple fractional volume formula
Circumradius (RK)
Circumradius with √2 factor
Inradius (RI)
Inradius with √5 dependency
Cubic-Pyramid Structure
Base structure with edge a
One on each cube face
4 triangles per pyramid
Structure: Cube + 6 identical pyramids = 24 isosceles triangular faces
Calculation Example for a Tetrakis Hexahedron
Given
Find: All properties of the cubic pyramid master
1. Surface Area Calculation
The surface area is 671 square units
2. Volume Calculation
The volume is 1500 cubic units
3. Pyramid Edge & Height
Pyramid edge: 7.5, Height: 15 units
4. Radii
Circumradius: 7.07, Inradius: 6.71 units
5. The Cubic Pyramid Master
The cubic pyramid master with perfect geometric simplicity
The Tetrakis Hexahedron: The Cubic Pyramid Master
The Tetrakis Hexahedron represents one of the most conceptually clear and mathematically accessible among the Catalan solids, demonstrating how simple geometric additions can create sophisticated polyhedral forms. Constructed by placing identical pyramids on each face of a cube, it transforms the familiar cubic form into a complex polyhedron with 24 triangular faces while maintaining mathematical simplicity through straightforward fractional relationships. As the dual to the truncated octahedron, it bridges the gap between elementary cubic geometry and advanced polyhedral theory, making it an ideal educational tool for understanding how Catalan solids emerge from systematic modifications of basic geometric forms.
The Cubic Foundation
The Tetrakis Hexahedron showcases cubic-pyramid mathematics:
- Cubic Base: Central cube with edge length a as the foundation
- Pyramid Addition: Six identical pyramids, one on each cube face
- 24 Triangular Faces: Four isosceles triangles per pyramid
- Simple Ratios: All measurements in simple fractions of a
- Clear Construction: Easy to visualize and build physically
- Educational Value: Perfect for teaching polyhedral concepts
- Mathematical Accessibility: Formulas involve only basic operations
Catalan Heritage and Structural Clarity
Catalan Simplicity
Among the 13 Catalan solids, the Tetrakis Hexahedron stands out for its conceptual clarity. The cubic foundation makes it immediately comprehensible, while the pyramid additions demonstrate how complex forms emerge from simple additions.
Structural Transparency
The construction method (cube + pyramids) is so clear that students can easily build physical models, making it an excellent hands-on learning tool for understanding three-dimensional geometry.
Mathematical Elegance
The formulas demonstrate beautiful simplicity: pyramid edge b = 3a/4, height h = 3a/2, and volume V = 3a³/2. These straightforward relationships make calculations easy and memorable.
Educational Excellence
As a bridge between elementary cubic geometry and advanced polyhedral theory, it provides the perfect stepping stone for students progressing from basic shapes to complex mathematical forms.
The Mathematics of Construction
The Tetrakis Hexahedron demonstrates elegant mathematical relationships:
Fractional Relationships
All dimensions relate to the cube edge through simple fractions: pyramid edge = 3a/4, height = 3a/2. These relationships make the polyhedron mathematically predictable and educationally valuable.
Volume Simplicity
The volume V = 3a³/2 = 1.5a³ is remarkably simple, representing the original cube (a³) plus half again as much from the six pyramids. This intuitive relationship aids in understanding.
Surface Area Logic
The surface area A = 3√5·a² involves only the simple √5 factor, avoiding the complex nested radicals found in more advanced Catalan solids while still providing mathematical interest.
Constructive Geometry
The clear construction method (cube + pyramids) provides an excellent example of how complex polyhedra can emerge from systematic geometric operations on simpler forms.
Educational and Practical Significance
The Tetrakis Hexahedron serves important educational and practical purposes:
- Mathematics Education: Ideal introduction to Catalan solids and polyhedral geometry
- 3D Modeling: Simple enough for beginning CAD users yet interesting for advanced applications
- Architectural Elements: Practical for decorative and structural design applications
- Materials Science: Model for understanding cubic crystal modifications
- Manufacturing: Easy to produce with standard machining or 3D printing
- Art Projects: Accessible for students and artists working with geometric forms
- Physical Models: Perfect for hands-on geometry education
Construction and Manufacturing
Simple Construction
The clear geometric construction (cube + pyramids) makes physical building straightforward. Students can easily create models using cardboard, wood, or 3D printing with minimal mathematical complexity.
Manufacturing Friendly
The simple mathematical relationships translate to easy manufacturing tolerances and quality control. All measurements derive from simple fractions of the cube edge length.
Scalable Design
The fractional relationships remain constant at any scale, making the design equally suitable for small educational models and large architectural applications.
Cost Effective
The mathematical simplicity reduces computational complexity in CAD systems and minimizes the precision requirements in manufacturing, making it economically attractive.
Cultural and Artistic Impact
Educational Icon
The Tetrakis Hexahedron has become an educational icon for demonstrating how complex forms emerge from simple geometric operations, making abstract mathematical concepts tangible and understandable.
Artistic Accessibility
Artists appreciate its balance of geometric sophistication and constructional simplicity, making it popular for sculptures, installations, and decorative elements that need to be both beautiful and buildable.
Gateway Polyhedron
As a gateway to understanding more complex Catalan solids, it provides students and enthusiasts with confidence to explore advanced polyhedral geometry through its approachable mathematics.
Design Applications
Architects and designers value its clear geometric logic and practical constructibility, making it suitable for both theoretical design studies and actual construction projects.
Summary
The Tetrakis Hexahedron stands as the most educationally valuable and practically accessible of all Catalan solids, demonstrating how sophisticated geometric forms can emerge from simple, systematic modifications of basic shapes. Its clear construction method (cube + pyramids), straightforward mathematical relationships, and practical buildability make it an ideal bridge between elementary geometry and advanced polyhedral theory. From its role in mathematics education to its applications in art, architecture, and manufacturing, it exemplifies how mathematical beauty and practical utility can coexist in perfect harmony. As both a teaching tool and a design element, the Tetrakis Hexahedron continues to inspire students, educators, artists, and engineers with its elegant demonstration that complexity and clarity need not be mutually exclusive in geometric design.