Hexakis Octahedron Calculator
Calculator and formulas for calculating a hexakis octahedron
Hexakis Octahedron Calculator
The Hexakis Octahedron
A Hexakis Octahedron is a Catalan solid with 48 irregular triangular faces - dual to the truncated cuboctahedron.
Hexakis Octahedron Properties
The Complex Cubic Body: Dual to the truncated cuboctahedron
Hexakis Octahedron Structure
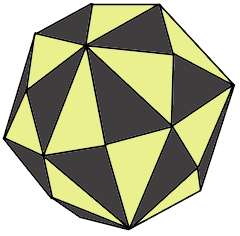
The complex cubic body with 48 triangular faces.
Dual to the truncated cuboctahedron.
|
|
What is a Hexakis Octahedron?
A Hexakis Octahedron is a complex Catalan solid with cubic-derived symmetry:
- Definition: Polyhedron with 48 irregular triangular faces
- Faces: Each face is a scalene triangle
- Dual: To the truncated cuboctahedron
- Vertices: 26 vertices with different coordination
- Edges: 72 edges in three lengths
- Symmetry: Octahedral symmetry group
Geometric Properties of the Hexakis Octahedron
The Hexakis Octahedron exhibits complex cubic-derived geometric properties:
Basic Parameters
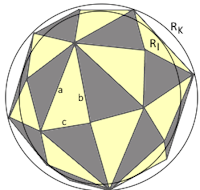
- Edge Lengths: Three different edge lengths a, b, c
- Faces: 48 congruent scalene triangles
- Euler Characteristic: V - E + F = 26 - 72 + 48 = 2
- Dual Form: Truncated cuboctahedron
Complex Properties
- Catalan Solid: Dual to Archimedean solid
- Triangular Faces: Each face is a scalene triangle
- Square Root 2 Geometry: Proportions contain √2
- Octahedral Symmetry: 48 symmetry operations
Mathematical Relationships
The Hexakis Octahedron follows complex mathematical laws with √2 relationships:
Volume Formula
Complex formula with nested √2 terms. Coefficient ≈ 3.76 from octahedral geometry.
Surface Area Formula
Sum of 48 scalene triangles. Square root 2 geometry in complex form.
Applications of the Hexakis Octahedron
Hexakis Octahedra find applications in complex structural analysis:
Scientific Research
- Complex crystallography studies
- Molecular cage structures
- Octahedral coordination chemistry
- Materials science applications
Engineering
- Complex 3D modeling challenges
- Structural analysis applications
- Precision measurement systems
- CAD software testing
Education
- Advanced geometry education
- Catalan solid studies
- Duality demonstrations
- √2 geometry relationships
Art & Design
- Complex sculptural forms
- Geometric art installations
- Architectural design elements
- Mathematical art projects
Formulas for the Hexakis Octahedron
Long Edge (a)
Relationship between long and medium edges
Medium Edge (b)
Medium edge in terms of long edge
Short Edge (c)
Short edge relationship with √2
Surface Area (S)
Surface area with √2 dependencies
Volume (V)
Volume with complex nested radicals
Circumradius (RK)
Circumradius with √2 factor
Inradius (RI)
Inradius with complex √2 dependency
Calculation Example for a Hexakis Octahedron
Given
Find: All properties of the complex cubic body
1. Surface Area Calculation
The surface area is 1206 square units
2. Volume Calculation
The volume is 3760 cubic units
3. Edge Length Ratios
Medium edge: 8.20, Short edge: 6.13 units
4. Radii
Circumradius: 9.57, Inradius: 9.35 units
5. The Complex Cubic Body
The complex cubic body with sophisticated mathematical relationships
The Hexakis Octahedron: The Complex Cubic Body
The Hexakis Octahedron represents a fascinating intermediate complexity among the Catalan solids, bridging the gap between simpler cubic forms and the ultimate complexity of icosahedral polyhedra. With its 48 scalene triangular faces arranged in octahedral symmetry, it demonstrates how cubic-derived mathematics can produce sophisticated geometric forms. As the dual solid to the truncated cuboctahedron, it embodies the principles of duality while maintaining the characteristic √2 relationships that permeate all cubic geometry, making it an excellent study object for understanding the transition from simple to complex polyhedral forms.
The Complexity of 48 Triangular Faces
The Hexakis Octahedron achieves remarkable geometric sophistication:
- 48 Triangular Faces: Each face is a scalene triangle with three different edge lengths
- Octahedral Symmetry: 48 symmetry operations derived from cubic geometry
- Three Edge Types: Long edge (a), medium edge (b), and short edge (c) in √2 ratios
- Complex Coordination: 26 vertices with varying coordination numbers
- Square Root 2 Mathematics: All proportions based on √2 ≈ 1.414
- Sophisticated Duality: Each triangular face corresponds to a vertex of the dual
- Intermediate Complexity: More complex than simple Catalan solids, less than icosahedral forms
Catalan Heritage and Octahedral Duality
Catalan Sophistication
As one of the 13 Catalan solids, the Hexakis Octahedron demonstrates intermediate complexity in the family. It shows how octahedral symmetry can create sophisticated face arrangements while maintaining the fundamental duality principle.
Octahedral Duality
As the dual to the truncated cuboctahedron, it transforms the complex vertex arrangements of its Archimedean partner into a uniform pattern of scalene triangular faces, demonstrating the power of polyhedral duality.
Geometric Balance
With 48 faces, it achieves a perfect balance between geometric complexity and mathematical tractability, making it ideal for studying advanced polyhedral relationships without overwhelming computational complexity.
Mathematical Elegance
The formulas, while complex, maintain the elegant √2 relationships characteristic of cubic geometry, making them more accessible than the golden ratio complexities of icosahedral forms.
The Square Root 2 Foundation
The Hexakis Octahedron is built upon √2 mathematical relationships:
Cubic Proportions
The three edge lengths follow precise √2-based ratios: a : b : c ≈ 1.22 : 1 : 0.61, all derivable from the fundamental cubic relationship involving √2 that underlies octahedral geometry.
Root-2 Formulas
All geometric formulas contain √2 terms in various combinations, reflecting the octahedral symmetry's basis in cubic geometry and distinguishing it from both simpler cubic and more complex icosahedral forms.
Octahedral Harmony
The arrangement of 48 triangular faces follows the laws of octahedral symmetry, creating a harmonious structure where each face relates to all others through precise √2-based geometric relationships.
Structural Efficiency
The octahedral organization provides excellent structural efficiency while maintaining the characteristic scalene triangle properties that make each face geometrically interesting and mathematically significant.
Scientific and Educational Significance
The Hexakis Octahedron serves important roles in various fields:
- Crystallography: Model for complex octahedral crystal structures and coordination compounds
- Materials Science: Template for advanced material structures with octahedral symmetry
- Educational Mathematics: Ideal for teaching intermediate polyhedral geometry concepts
- Structural Engineering: Reference for complex structural analysis problems
- Computer Graphics: Benchmark for intermediate 3D modeling algorithms
- Scientific Visualization: Standard for testing complex geometric rendering systems
- Geometric Art: Foundation for sophisticated mathematical art installations
Construction and Precision Requirements
Intermediate Precision
Manufacturing requires significant precision in creating 48 scalene triangles with three different edge lengths. While challenging, it's more manageable than icosahedral forms due to the rational √2 relationships.
Computational Accessibility
The √2-based mathematics makes calculations more straightforward than golden ratio forms, allowing for precise computation without the transcendental complexities of pentagonal geometry.
Manufacturing Feasibility
Modern CNC and 3D printing technologies can readily achieve the required precision for accurate physical models, making it accessible for educational and research applications.
Quality Control
The octahedral symmetry simplifies verification procedures, as the √2 relationships can be easily measured and confirmed with standard precision instruments.
Educational and Aesthetic Value
Perfect Teaching Tool
The Hexakis Octahedron serves as an ideal intermediate step in polyhedral education, complex enough to be challenging yet simple enough to be fully understood and calculated by advanced students.
Mathematical Beauty
The combination of 48 identical scalene triangles in octahedral arrangement creates a visually striking form that demonstrates how mathematical precision can produce aesthetic appeal.
Research Value
As a model system, it provides insights into the behavior of intermediate-complexity polyhedra, bridging the gap between simple and ultimate geometric forms.
Cultural Impact
In contemporary design culture, it represents the harmony achievable between mathematical sophistication and practical realizability, making it popular in architectural and artistic applications.
Summary
The Hexakis Octahedron stands as an exemplary intermediate Catalan solid that perfectly balances geometric complexity with mathematical accessibility. Its 48 scalene triangular faces, arranged in octahedral symmetry and governed by √2 relationships, make it an ideal study object for understanding advanced polyhedral geometry. From its role as the dual to the truncated cuboctahedron to its applications in materials science and education, it demonstrates how intermediate complexity can provide both intellectual challenge and practical utility. As a bridge between simple cubic forms and ultimate icosahedral complexity, the Hexakis Octahedron remains an essential polyhedron for students, researchers, and artists seeking to understand the sophisticated beauty that emerges from mathematical precision in three-dimensional space.