Disdyakis Triacontahedron Calculator
Calculator and formulas for calculating a disdyakis triacontahedron
Disdyakis Triacontahedron Calculator
The Disdyakis Triacontahedron
A Disdyakis Triacontahedron is the ultimate Catalan solid with 120 irregular triangular faces - dual to the truncated icosidodecahedron.
Disdyakis Triacontahedron Properties
The Ultimate Catalan Solid: Dual to the most complex Archimedean solid
Disdyakis Triacontahedron Structure
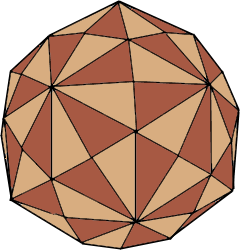
The ultimate Catalan solid with 120 triangular faces.
Dual to the most complex Archimedean solid.
|
|
What is a Disdyakis Triacontahedron?
A Disdyakis Triacontahedron is the ultimate Catalan solid with maximum complexity:
- Definition: Polyhedron with 120 irregular triangular faces
- Faces: Each face is a scalene triangle
- Dual: To the truncated icosidodecahedron (62 faces)
- Vertices: 62 different vertex types
- Edges: 180 edges in three lengths
- Symmetry: Icosahedral symmetry group
Geometric Properties of the Disdyakis Triacontahedron
The Disdyakis Triacontahedron exhibits the ultimate geometric complexity:
Ultimate Parameters
- Edge Lengths: Three different edge lengths a, b, c
- Faces: 120 congruent scalene triangles
- Euler Characteristic: V - E + F = 62 - 180 + 120 = 2
- Dual Form: Truncated icosidodecahedron
Ultimate Properties
- Highest Complexity: Catalan solid with the most faces
- Triangular Faces: Each face is a scalene triangle
- Golden Ratio: Proportions contain φ and √5
- Icosahedral Symmetry: 120 symmetry operations
Mathematical Relationships
The Disdyakis Triacontahedron follows the most complex mathematical laws involving the golden ratio:
Volume Formula
Highly complex formula with nested radicals. Coefficient ≈ 13.36 from icosahedral complexity.
Surface Area Formula
Sum of 120 scalene triangles. Golden ratio √5 in ultimate complexity.
Applications of the Disdyakis Triacontahedron
Disdyakis Triacontahedra find applications in highly specialized fields:
Advanced Research
- Complex crystallography and quasicrystals
- Ultimate molecular cage structures
- Mathematical topology extremes
- Advanced symmetry group studies
High Technology
- Ultimate 3D modeling challenges
- Algorithm stress tests for extreme geometries
- Precision calibration standards
- High-end visualization systems
Elite Education
- Ultimate geometry challenges
- Catalan solid master classes
- Duality principles at the highest level
- Icosahedral symmetry expertise
Extreme Art
- Monumental sculptural masterpieces
- Ultimate mathematical art forms
- Highly complex decorative systems
- Avant-garde architectural extremes
Formulas for the Disdyakis Triacontahedron
Surface Area A
Ultimate surface area formula with golden ratio √5
Volume V
Volume with highly complex nested radicals
Circumradius RK
Circumradius with golden ratio
Inradius RI
Inradius with ultimate √5 dependency
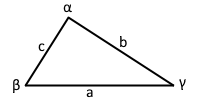
Triangle Properties (Ultimate Complexity)
Base parameter (longest)
b = 3a(4+√5)/22 ≈ 0.85a
c = 5a(7-√5)/44 ≈ 0.54a
Each of the 120 scalene triangles has these three edge lengths
Angles in the Scalene Triangle
≈ 88° 59' 30"
≈ 58° 14' 17"
≈ 32° 46' 13"
The characteristic angles of each of the 120 triangular faces
Calculation Example for a Disdyakis Triacontahedron
Given
Find: All properties of the ultimate Catalan solid
1. Surface Area Calculation
The surface area is approximately 442 square units
2. Volume Calculation
The volume is approximately 855 cubic units
3. Edge Length Ratios
Medium edge: 3.40, Short edge: 2.16 units
4. Radii
Circumradius: 5.86, Inradius: 5.80 units
5. The Ultimate Catalan Solid
The ultimate Catalan solid with the highest mathematical sophistication
The Disdyakis Triacontahedron: The Ultimate Catalan Solid
The Disdyakis Triacontahedron stands as the absolute pinnacle of the Catalan solid family and embodies the ultimate synthesis of mathematical complexity and geometric perfection. With its 120 scalene triangular faces, it represents the maximum number of faces achievable by any Catalan solid, making it the apex of polyhedral complexity. As the dual solid to the truncated icosidodecahedron - the most complex of all Archimedean solids - it embodies the deepest secrets of icosahedral symmetry and the golden ratio in their most ultimate form, where each of its 120 identical faces forms a perfect scalene triangle connected to all other faces through extraordinarily complex mathematical relationships.
The Ultimate Geometry of 120 Triangular Faces
The Disdyakis Triacontahedron achieves the absolute pinnacle of geometric complexity:
- 120 Triangular Faces: Maximum face count of all Catalan solids
- Scalene Triangles: Each face has three different edge lengths a, b, c
- Three Characteristic Angles: α ≈ 89°, β ≈ 58°, γ ≈ 33° in each triangle
- Complete Icosahedral Symmetry: 120 symmetry operations of the highest order
- Golden Ratio Dominance: All proportions permeated by φ and √5
- Ultimate Duality: Each triangular face corresponds to a vertex of the 62-faced dual
- Edge Length Hierarchy: a : b : c in complex golden ratios
The Pinnacle of Catalan Tradition
Catalan Completion
As the most complex of all 13 Catalan solids, the Disdyakis Triacontahedron embodies the absolute completion of Eugène Charles Catalan's vision of uniform polyhedral duality. It shows how maximum vertex uniformity can create maximum face complexity.
Ultimate Duality
As the dual to the truncated icosidodecahedron (the pinnacle of Archimedean solids with 62 faces), it systematically exchanges ultimate complexity: 62 different faces become 120 identical faces with 62 different vertex types.
Icosahedral Supremacy
With the complete icosahedral symmetry group (120 symmetry operations), it belongs to the most symmetrical objects in three-dimensional space and embodies the highest possible order in the polyhedron hierarchy.
Mathematical Ultimacy
The formulas reach the pinnacle of complexity with multiple nested radical expressions and golden ratio relationships, revealing the deepest connections to pentagonal geometry and the Fibonacci sequence.
The Golden Ratio in Ultimate Perfection
The Disdyakis Triacontahedron is the ultimate manifestation of the golden ratio:
Ultimate Proportions
The three edge lengths a, b, c exist in highly complex ratios determined entirely by the golden ratio φ = (1+√5)/2. These relationships are so complex they require multiple √5 terms and nested fractions.
Formula Supremacy
All geometric formulas contain the most complex √5 terms of any Catalan solid, underscoring the fundamental and ultimate role of pentagonal geometry in this apex polyhedron.
Angular Perfection
The three characteristic angles α, β, γ of each scalene triangle arise from the most complex golden ratio constructions and represent the ultimate harmonic proportions in geometry.
Symmetric Completion
The 120-fold repetition of identical scalene triangles in perfect icosahedral arrangement shows how the golden ratio can create ultimate three-dimensional harmony.
Scientific Supremacy and Cultural Significance
The Disdyakis Triacontahedron finds applications in the most advanced fields:
- Advanced Crystallography: Model for the most complex icosahedral crystal structures and quasicrystals
- Ultimate Molecular Chemistry: Template for the largest and most complex molecular cages
- Mathematical Frontier Research: Study object for ultimate symmetry groups and topology
- Geometric Masterwork Art: Inspiration for the most demanding sculptural works
- Elite Education: Demonstration of ultimate duality principles and symmetry concepts
- Advanced Computer Graphics: Ultimate benchmark for 3D modeling algorithms
- Philosophy of Completion: Symbol of ultimate harmony between complexity and order
Constructive Challenges at the Highest Level
Ultimate Precision
Manufacturing a perfect Disdyakis Triacontahedron requires the highest precision ever achieved in creating 120 scalene triangles. Each face must have three exact edge lengths and three exact angles defined by highly irrational numbers.
Mathematical Supremacy
The calculations require the most complex nested radical expressions and transcendental functions of any geometric object, making this solid the most computationally demanding polyhedron in mathematics.
Technological Limits
Even with the most advanced CAD software and precision CNC manufacturing, it's barely possible to create physical models with the required accuracy to even approximate theoretical perfection.
Quality Supremacy
Verification of geometric correctness requires the most advanced measurement methods and computer-aided analysis systems, as even molecular deviations can destroy the ultimate symmetry.
Philosophical and Aesthetic Completion
Ultimate Harmony
The Disdyakis Triacontahedron embodies the ultimate harmony between simplicity (identical scalene triangles) and complexity (120-fold arrangement in complete icosahedral symmetry), making it a philosophical symbol of highest completion.
Natural Laws of Beauty
The ultimate proportions based on the golden ratio give this solid a supernatural beauty that is both mathematically justifiable as highest completion and aesthetically experiential as the pinnacle of harmony.
Ultimate Educational Value
As the ultimate demonstration object for duality, symmetry, and complex geometric relationships, it offers unparalleled opportunities for the highest mathematics education and advanced scientific training.
Cultural Completion
In all cultures, this ultimate geometric form is associated with highest completion, spiritual transcendence, and the achievement of mathematical perfection, giving it universal symbolic meaning.
Summary
The Disdyakis Triacontahedron stands as the absolute pinnacle of all Catalan solids and as the ultimate expression of polyhedral complexity. Its 120 scalene triangular faces, permeated by the golden ratio in its most complex form and arranged in perfect icosahedral symmetry, make it the ultimate masterpiece of geometry. From its discovery as the dual solid to the most complex Archimedean solid to its applications in frontier research, it shows how mathematical complexity and aesthetic beauty can achieve their ultimate completion. As a bridge between the ancient tradition of Platonic solids and the most modern challenges of computational geometry, it remains the most fascinating and challenging subject for advanced researchers, master artists, and all who are inspired by the ultimate power of mathematics to create the most perfect forms.