Deltoidalhexakontaeder Rechner
Rechner und Formeln zur Berechnung eines Deltoidalhexakontaeder
Deltoidalhexakontaeder Rechner
Das Deltoidalhexakontaeder
Ein Deltoidalhexakontaeder ist ein katalanischer Körper mit 60 drachenförmigen Deltoidflächen.
Deltoidalhexakontaeder Struktur
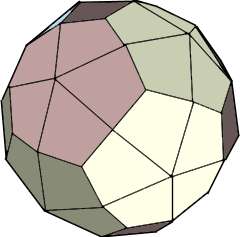
Der faszinierende Drachen-Körper mit 60 Deltoidflächen.
Dual zum Rhombenikosidodekaeder.
|
|
Was ist ein Deltoidalhexakontaeder?
Ein Deltoidalhexakontaeder ist ein faszinierender katalanischer Körper:
- Definition: Polyeder mit 60 Deltoidflächen (Drachenvierecken)
- Flächen: Jede Fläche ist ein konvexes Viereck (Deltoid)
- Dual: Zum Rhombenikosidodekaeder (archimedischer Körper)
- Ecken: 62 identische Ecken
- Kanten: 120 Kanten in zwei Längen
- Symmetrie: Ikosaedrische Symmetriegruppe
Geometrische Eigenschaften des Deltoidalhexakontaeders
Das Deltoidalhexakontaeder zeigt bemerkenswerte geometrische Eigenschaften:
Grundparameter
- Kantenlängen: Zwei verschiedene Kantenlängen a und b
- Flächen: 60 kongruente Deltoidflächen
- Euler-Charakteristik: V - E + F = 62 - 120 + 60 = 2
- Dualform: Rhombenikosidodekaeder
Besondere Eigenschaften
- Katalanischer Körper: Dual zu archimedischem Körper
- Deltoidflächen: Jede Fläche ist ein Drachenviereck
- Goldener Schnitt: Proportionen enthalten φ
- Ikosaedrische Symmetrie: 120 Symmetrieoperationen
Mathematische Beziehungen
Das Deltoidalhexakontaeder folgt komplexen mathematischen Gesetzen mit dem goldenen Schnitt:
Volumenformel
Komplexe Formel mit verschachtelten Wurzeln. Koeffizient ≈ 22.21 aus ikosaedrischer Geometrie.
Oberflächenformel
Summe von 60 Deltoidflächen. Goldener Schnitt √5 in komplexer Form.
Anwendungen des Deltoidalhexakontaeders
Deltoidalhexakontaeder finden Anwendung in spezialisierten Bereichen:
Wissenschaft & Forschung
- Kristallographie und Mineralstruktur-Analyse
- Komplexe Molekülkäfig-Strukturen
- Mathematische Topologie-Studien
- Symmetriegruppen-Theorie
Technik & Design
- 3D-Modellierung und Computergrafik
- Algorithmus-Tests für komplexe Geometrien
- Architektonische Gestaltungselemente
- Mathematische Visualisierungswerkzeuge
Bildung & Lehre
- Geometrie-Unterricht und Demonstrationen
- Katalanische Körper Studien
- Dualitäts-Prinzipien in der Mathematik
- Symmetrie und Gruppentheorie
Kunst & Gestaltung
- Skulpturale Installationen
- Mathematische Kunst und Design
- Dekorative Muster und Motive
- Architektonische Ornamente
Formeln für das Deltoidalhexakontaeder
Oberfläche A
Oberfläche mit goldenem Schnitt √5
Volumen V
Volumen mit komplexen verschachtelten Wurzeln
Kantenradius RK
Kantenradius mit goldenem Schnitt
Innenradius RI
Innenradius mit √5-Abhängigkeit
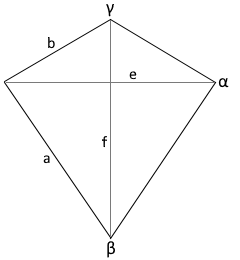
Deltoid-Eigenschaften
Grundparameter
b ≈ a/1.54
e ≈ 1.115·a
f ≈ 1.163·a
Jede der 60 Deltoidflächen hat diese Eigenschaften
Winkel im Deltoid
≈ 86° 58' 27"
≈ 67° 46' 59"
≈ 118° 16' 7"
Die charakteristischen Winkel jeder Deltoidfläche
Berechnungsbeispiel für ein Deltoidalhexakontaeder
Gegeben
Gesucht: Alle Eigenschaften des Drachen-Körpers
1. Oberflächenberechnung
Die Oberfläche beträgt etwa 156 Flächeneinheiten
2. Volumenberechnung
Das Volumen beträgt etwa 178 Kubikeinheiten
3. Kantenradius
Der Kantenradius beträgt etwa 3.51 Einheiten
4. Innenradius
Der Innenradius beträgt etwa 3.42 Einheiten
5. Deltoid-Eigenschaften
Der faszinierende Drachen-Körper mit komplexer mathematischer Schönheit
Das Deltoidalhexakontaeder: Der geheimnisvolle Drachen-Körper
Das Deltoidalhexakontaeder ist einer der faszinierendsten und geheimnisvollsten unter den katalanischen Körpern. Mit seinen 60 drachenförmigen Deltoidflächen verkörpert es eine einzigartige Verbindung zwischen mathematischer Komplexität und geometrischer Eleganz. Als dualer Körper zum Rhombenikosidodekaeder repräsentiert es die tiefsten Geheimnisse der ikosaedrischen Symmetrie und des goldenen Schnitts, wobei jede seiner 60 identischen Flächen ein perfektes Drachenviereck darstellt, das durch komplexe mathematische Beziehungen mit allen anderen Flächen verbunden ist.
Die Geometrie der Deltoidflächen
Das Deltoidalhexakontaeder fasziniert durch seine einzigartigen Flächeneigenschaften:
- 60 Deltoidflächen: Jede Fläche ist ein konvexes Drachenviereck mit zwei Paar gleichen Seiten
- Zwei Kantenlängen: Jedes Deltoid hat eine lange Kante (a) und eine kurze Kante (b)
- Charakteristische Winkel: Seitenwinkel ≈ 87°, Fußwinkel ≈ 68°, Kopfwinkel ≈ 118°
- Symmetrieachsen: Jedes Deltoid hat eine Symmetrieachse durch die beiden Ecken unterschiedlicher Winkel
- Goldener Schnitt: Alle Proportionen basieren auf dem goldenen Schnitt φ = (1+√5)/2
- Perfekte Anordnung: Die 60 Deltoide fügen sich zu einem vollkommen symmetrischen Körper zusammen
- Dualitätsprinzip: Jede Deltoidfläche entspricht einer Ecke des dualen Rhombenikosidodekaeders
Katalanische Körper und Dualität
Katalanische Tradition
Benannt nach Eugène Charles Catalan (1814-1894), gehört dieses Polyeder zu den 13 katalanischen Körpern - den dualen Formen der archimedischen Körper. Es zeigt, wie aus uniformen Ecken kongruente Flächen entstehen können.
Dualitätsprinzip
Als Dual zum Rhombenikosidodekaeder (mit 62 Ecken, 120 Kanten, 60 Flächen) vertauscht es systematisch Ecken und Flächen: 60 Flächen werden zu 60 Ecken, während die Kantenzahl gleich bleibt.
Ikosaedrische Symmetrie
Mit der vollen ikosaedrischen Symmetriegruppe (120 Symmetrieoperationen) gehört es zu den symmetrischsten dreidimensionalen Formen überhaupt, was seine faszinierende geometrische Perfektion erklärt.
Mathematische Komplexität
Die Formeln enthalten mehrfach verschachtelte Wurzelausdrücke mit dem goldenen Schnitt, was die tiefe Verbindung zur pentagonalen Geometrie und zur Fibonacci-Folge zeigt.
Der goldene Schnitt in der Deltoid-Geometrie
Das Deltoidalhexakontaeder ist durchdrungen vom goldenen Schnitt:
Proportionsverhältnisse
Das Verhältnis der langen zur kurzen Kante beträgt etwa 1.54, was eng mit dem goldenen Schnitt φ ≈ 1.618 verwandt ist. Diese Proportion sorgt für die harmonische Erscheinung der Deltoidflächen.
Formelstrukturen
Praktisch alle geometrischen Formeln enthalten √5-Terme, die direkt mit dem goldenen Schnitt zusammenhängen: φ = (1+√5)/2. Dies zeigt die fundamentale Rolle der pentagonalen Geometrie.
Winkelbeziehungen
Die charakteristischen Winkel der Deltoidflächen entstehen durch Konstruktionen, die auf dem goldenen Schnitt basieren und damit zu den harmonischsten Proportionen in der Geometrie gehören.
Symmetrische Perfektion
Die 60-fache Wiederholung identischer Deltoidflächen in perfekter ikosaedrischer Anordnung zeigt, wie der goldene Schnitt dreidimensionale Harmonie erzeugen kann.
Wissenschaftliche und kulturelle Bedeutung
Das Deltoidalhexakontaeder findet Anwendung in verschiedenen Bereichen:
- Kristallographie: Modell für komplexe Kristallstrukturen mit ikosaedrischer Symmetrie
- Molekularchemie: Template für große Molekülkäfige und Fullerene-Derivate
- Mathematische Forschung: Studienobjekt für Symmetriegruppen und Topologie
- Geometrische Kunst: Inspiration für skulpturale Werke und Architektur
- Bildungswesen: Demonstration von Dualitätsprinzipien und Symmetrikonzepten
- Computergrafik: Benchmark für komplexe 3D-Modellierungsalgorithmen
- Philosophie: Symbol für die Harmonie zwischen Komplexität und Ordnung
Konstruktion und mathematische Herausforderungen
Konstruktive Schwierigkeiten
Die Herstellung eines perfekten Deltoidalhexakontaeders erfordert höchste Präzision bei der Fertigung der 60 Deltoidflächen. Jede Fläche muss exakte Winkel und Kantenlängen aufweisen, die durch irrationale Zahlen definiert sind.
Mathematische Komplexität
Die Berechnungen erfordern mehrfach verschachtelte Wurzelausdrücke und transzendente Funktionen, was diesen Körper zu einem der rechnerisch anspruchsvollsten geometrischen Objekte macht.
Moderne Technologie
Erst mit moderner CAD-Software und Präzisionsfertigung ist es möglich geworden, physische Modelle mit der erforderlichen Genauigkeit herzustellen, um die theoretische Perfektion zu realisieren.
Qualitätskontrolle
Die Verifikation der geometrischen Korrektheit erfordert hochpräzise Messverfahren und computergestützte Analysesysteme, da bereits kleinste Abweichungen die Symmetrie zerstören können.
Philosophische und ästhetische Dimensionen
Harmonie der Gegensätze
Das Deltoidalhexakontaeder verkörpert die Harmonie zwischen Einfachheit (identische Deltoidflächen) und Komplexität (60-fache Anordnung in ikosaedrischer Symmetrie), was es zu einem philosophischen Symbol macht.
Natürliche Schönheit
Die auf dem goldenen Schnitt basierenden Proportionen verleihen diesem Körper eine natürliche Schönheit, die sowohl mathematisch begründet als auch ästhetisch ansprechend ist.
Bildungswert
Als Demonstrationsobjekt für Dualität, Symmetrie und komplexe geometrische Beziehungen bietet es unvergleichliche Möglichkeiten für den Mathematikunterricht und die Wissenschaftskommunikation.
Kulturelle Symbolik
In verschiedenen Kulturen werden drachenförmige Strukturen mit Harmonie, Ausgewogenheit und spiritueller Vollendung assoziiert, was diesem Körper zusätzliche symbolische Bedeutung verleiht.
Zusammenfassung
Das Deltoidalhexakontaeder steht als einer der geheimnisvollsten und mathematisch anspruchsvollsten katalanischen Körper da. Seine 60 drachenförmigen Deltoidflächen, durchdrungen vom goldenen Schnitt und arrangiert in perfekter ikosaedrischer Symmetrie, machen es zu einem Meisterwerk der Geometrie. Von seiner Entdeckung als dualer Körper zum Rhombenikosidodekaeder bis zu seinen modernen Anwendungen in Wissenschaft und Kunst zeigt es, wie mathematische Komplexität und ästhetische Schönheit eine untrennbare Einheit bilden können. Als Bindeglied zwischen der antiken Tradition der platonischen Körper und den modernen Herausforderungen der computational geometry bleibt es ein faszinierender Gegenstand für Forscher, Künstler und alle, die von der Macht der Mathematik zur Erschaffung vollkommener Formen begeistert sind.