Deltoidalikositetraeder Rechner
Rechner und Formeln zur Berechnung eines Deltoidalikositetraeder
Deltoidalikositetraeder Rechner
Das Deltoidalikositetraeder
Ein Deltoidalikositetraeder ist ein katalanischer Körper mit 24 drachenförmigen Deltoidflächen und kubischer Symmetrie.
Deltoidalikositetraeder Eigenschaften
Der Kompakte Drachen-Körper: Dual zum Rhombenabgeschrägten Kuboktaeder
Deltoidalikositetraeder Struktur
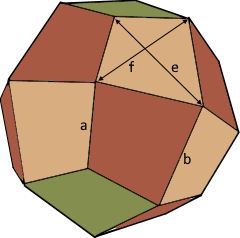
Der kompakte Drachen-Körper mit 24 Deltoidflächen.
Kubische Symmetrie mit perfekter Harmonie.
|
|
Was ist ein Deltoidalikositetraeder?
Ein Deltoidalikositetraeder ist ein kompakter katalanischer Körper mit kubischer Symmetrie:
- Definition: Polyeder mit 24 Deltoidflächen (Drachenvierecken)
- Flächen: Jede Fläche ist ein konvexes Drachenviereck
- Dual: Zum Rhombenabgeschrägten Kuboktaeder
- Ecken: 26 Ecken (8 dreifach + 18 vierfach)
- Kanten: 48 Kanten in zwei Längen
- Symmetrie: Kubische Symmetriegruppe
Geometrische Eigenschaften des Deltoidalikositetraeders
Das Deltoidalikositetraeder zeigt faszinierende kubische Eigenschaften:
Grundparameter
- Kantenlängen: Zwei verschiedene Kantenlängen a und b
- Flächen: 24 kongruente Deltoidflächen
- Euler-Charakteristik: V - E + F = 26 - 48 + 24 = 2
- Dualform: Rhombenabgeschrägtes Kuboktaeder
Kubische Eigenschaften
- Katalanischer Körper: Dual zu uniformem Polyeder
- Deltoidflächen: Jede Fläche ist ein Drachenviereck
- Wurzel 2 Geometrie: Proportionen enthalten √2
- Kubische Symmetrie: 48 Symmetrieoperationen
Mathematische Beziehungen
Das Deltoidalikositetraeder folgt kubischen mathematischen Gesetzen mit √2:
Volumenformel
Kubische Formel mit √2-Termen. Koeffizient ≈ 6.90 aus kubischer Geometrie.
Oberflächenformel
Summe von 24 Deltoidflächen. Wurzel 2 Geometrie in kompakter Form.
Anwendungen des Deltoidalikositetraeders
Deltoidalikositetraeder finden Anwendung in kubischen Strukturen:
Kubische Strukturen
- Kristallographie kubischer Systeme
- Architektonische modulare Elemente
- Kompakte Raumfüllung und Tessellation
- Metallische Gitterstrukturen
Ingenieurswesen
- Mechanische Komponenten mit kubischer Symmetrie
- 3D-Drucker Kalibrierungsobjekte
- Präzisions-Messwerkzeuge
- Robotik und Automatisierung
Mathematische Bildung
- Kubische Symmetrie Demonstrationen
- Katalanische Körper Studien
- Dualitätsprinzipien in der Geometrie
- √2-Geometrie und Wurzelbeziehungen
Design & Kunst
- Kubische Skulpturen und Installationen
- Geometrische Muster und Ornamente
- Modulare Designelemente
- Architektonische Fassadengestaltung
Formeln für das Deltoidalikositetraeder
Oberfläche A
Oberfläche mit √2-Termen aus kubischer Geometrie
Volumen V
Volumen mit kubischen √2-Beziehungen
Kantenradius RK
Einfache kubische Formel mit √2
Innenradius RI
Innenradius mit √2-Abhängigkeit
Deltoid-Eigenschaften (Kubische Version)
Grundparameter
b = a(4+√2)/7
e ≈ 1.17·a
f ≈ 1.31·a
Jede der 24 Deltoidflächen hat kubische √2-Proportionen
Kubische Kantenverhältnisse
a/b = 7/(4+√2) ≈ 1.29
Wurzel 2 dominiert alle Proportionen
Charakteristische √2-Beziehungen der kubischen Symmetrie
Berechnungsbeispiel für ein Deltoidalikositetraeder
Gegeben
Gesucht: Alle Eigenschaften des kompakten Drachen-Körpers
1. Oberflächenberechnung
Die Oberfläche beträgt etwa 165 Flächeneinheiten
2. Volumenberechnung
Das Volumen beträgt etwa 186 Kubikeinheiten
3. Kantenradius
Der Kantenradius beträgt etwa 3.62 Einheiten
4. Kurze Kante
Die kurze Kante beträgt etwa 2.32 Einheiten
5. Der Kubische Drachen-Körper
Der kompakte Drachen-Körper mit perfekter kubischer Harmonie
Das Deltoidalikositetraeder: Der kubische Drachen-Körper
Das Deltoidalikositetraeder ist ein faszinierender katalanischer Körper, der die Eleganz kubischer Symmetrie mit der komplexen Schönheit von Deltoidflächen verbindet. Mit seinen 24 drachenförmigen Flächen, die in perfekter kubischer Harmonie angeordnet sind, stellt es eine bemerkenswerte Synthese aus geometrischer Kompaktheit und mathematischer Raffinesse dar. Als dualer Körper zum rhombenabgeschrägten Kuboktaeder verkörpert es die tiefsten Prinzipien der kubischen Geometrie, wobei die charakteristische Wurzel-2-Mathematik alle seine Proportionen und Beziehungen durchdringt und ihm eine einzigartige Stellung unter den katalanischen Körpern verleiht.
Die kubische Harmonie der Deltoidflächen
Das Deltoidalikositetraeder fasziniert durch seine kubische Perfektion:
- 24 Deltoidflächen: Jede Fläche ist ein konvexes Drachenviereck mit kubischen Proportionen
- Kubische Symmetrie: Oktaedrische Symmetriegruppe mit 48 Symmetrieoperationen
- Zwei Kantenlängen: Lange Kante (a) und kurze Kante (b) im √2-Verhältnis
- Kompakte Struktur: 26 Ecken (8 dreifach, 18 vierfach) in optimaler Anordnung
- Wurzel-2-Geometrie: Alle Proportionen basieren auf √2 ≈ 1.414
- Perfekte Tessellation: Die 24 Deltoide fügen sich nahtlos zusammen
- Dualitätsprinzip: Jede Deltoidfläche entspricht einer Ecke des dualen Polyeders
Katalanische Tradition und kubische Dualität
Katalanische Eleganz
Als einer der 13 katalanischen Körper zeigt das Deltoidalikositetraeder, wie aus uniformen Ecken kongruente Flächen entstehen. Die kubische Symmetrie macht es zu einem besonders eleganten Vertreter dieser Familie.
Kubische Dualität
Als Dual zum rhombenabgeschrägten Kuboktaeder vertauscht es systematisch Ecken und Flächen, wobei die kubische Struktur erhalten bleibt und die √2-Beziehungen verstärkt werden.
Kompakte Perfektion
Mit nur 24 Flächen erreicht es eine bemerkenswerte strukturelle Kompaktheit, die es zu einem idealen Demonstrationsobjekt für kubische Symmetrie und Deltoid-Geometrie macht.
Mathematische Klarheit
Die Formeln sind durch die kubische Struktur relativ einfach und elegant, mit klaren √2-Beziehungen, die das Verständnis der zugrundeliegenden Geometrie erleichtern.
Die Wurzel-2-Geometrie der kubischen Ordnung
Das Deltoidalikositetraeder ist durchdrungen von √2-Beziehungen:
Kubische Proportionen
Das Verhältnis der langen zur kurzen Kante folgt der kubischen Beziehung a/b = 7/(4+√2) ≈ 1.29, die direkt aus der oktaedrischen Symmetrie des zugrunde liegenden Kubus hervorgeht.
Wurzel-2-Formeln
Praktisch alle geometrischen Formeln enthalten √2-Terme, die die fundamentale kubische Natur dieses Polyeders widerspiegeln und es von den φ-basierten ikosaedrischen Körpern unterscheiden.
Kubische Harmonie
Die Anordnung der 24 Deltoidflächen folgt den Gesetzen der kubischen Symmetrie, wodurch jede Fläche in perfekter Harmonie mit allen anderen steht und eine bemerkenswerte strukturelle Einheit entsteht.
Geometrische Effizienz
Die kubische Organisation ermöglicht eine außergewöhnlich effiziente Raumnutzung bei gleichzeitiger Beibehaltung der charakteristischen Deltoid-Eigenschaften jeder einzelnen Fläche.
Wissenschaftliche und technische Bedeutung
Das Deltoidalikositetraeder findet vielfältige Anwendungen:
- Kubische Kristallographie: Modell für komplexe kubische Kristallstrukturen
- Präzisionstechnik: Referenzobjekt für kubische Symmetrie-Messungen
- Architektur: Modulare Bauelemente mit kubischer Symmetrie
- Mechanik: Kompakte mechanische Komponenten mit Deltoid-Oberflächen
- Bildung: Ideales Lehrobjekt für kubische Geometrie und Dualität
- 3D-Druck: Kalibrierungsobjekt für Präzisions-3D-Drucker
- Materialwissenschaft: Template für kubische Gitterstrukturen
Konstruktion und kubische Präzision
Kubische Präzision
Die Herstellung erfordert höchste Präzision bei der Einhaltung der kubischen Symmetrie. Jede der 24 Deltoidflächen muss exakte √2-Proportionen aufweisen, um die Gesamtsymmetrie zu gewährleisten.
Fertigungsvorteile
Die kubische Struktur erleichtert die Fertigung, da die Grundorientierungen den Standard-Koordinatenachsen entsprechen und somit konventionelle Fertigungsverfahren optimal genutzt werden können.
Qualitätskontrolle
Die Überprüfung der kubischen Symmetrie kann mit Standard-Messgeräten erfolgen, was die Qualitätssicherung vereinfacht und eine kostengünstige Produktion ermöglicht.
Moderne Fertigung
CNC-Maschinen und 3D-Drucker können die kubischen Beziehungen präzise umsetzen, wodurch hochwertige physische Modelle für Forschung und Bildung realisierbar werden.
Ästhetische und pädagogische Dimensionen
Kubische Ästhetik
Die Kombination aus kubischer Ordnung und Deltoid-Eleganz erzeugt eine einzigartige ästhetische Wirkung, die sowohl mathematische Rationalität als auch organische Schönheit ausstrahlt.
Pädagogischer Wert
Als kompaktes Beispiel für katalanische Körper mit kubischer Symmetrie ist es ideal geeignet, um Studenten die Prinzipien der Dualität und √2-Geometrie zu vermitteln.
Symbolische Bedeutung
In der Designphilosophie symbolisiert es die perfekte Balance zwischen struktureller Effizienz und ästhetischer Raffinesse, zwischen mathematischer Ordnung und natürlicher Eleganz.
Kulturelle Relevanz
Als Vertreter der kubischen Familie geometrischer Formen verbindet es sich mit kulturellen Traditionen, die Ordnung, Stabilität und handwerkliche Präzision schätzen.
Zusammenfassung
Das Deltoidalikositetraeder verkörpert die perfekte Synthese aus kubischer Ordnung und Deltoid-Eleganz. Mit seinen 24 drachenförmigen Flächen, die in perfekter oktaedrischer Symmetrie angeordnet sind, zeigt es, wie mathematische Prinzipien geometrische Schönheit von bemerkenswerter Kompaktheit und Klarheit erzeugen können. Die durchgängigen √2-Beziehungen verbinden es tief mit der kubischen Geometrie und machen es zu einem idealen Studienobjekt für die Erforschung von Dualität, Symmetrie und den fundamentalen Prinzipien der dreidimensionalen Geometrie. Von seiner theoretischen Bedeutung in der reinen Mathematik bis zu seinen praktischen Anwendungen in Technik und Design bleibt das Deltoidalikositetraeder ein faszinierendes Beispiel dafür, wie elegante mathematische Strukturen sowohl intellektuelle Befriedigung als auch praktischen Nutzen bieten können.