Hexakisikosaeder Rechner
Rechner und Formeln zur Berechnung eines Hexakisikosaeder
Hexakisikosaeder Rechner
Das Hexakisikosaeder
Ein Hexakisikosaeder ist der ultimative katalanische Körper mit 120 unregelmäßigen Dreiecksflächen - dual zum Truncated Icosidodecahedron.
Hexakisikosaeder Eigenschaften
Der Ultimative Katalanische Körper: Dual zum komplexesten archimedischen Körper
Hexakisikosaeder Struktur
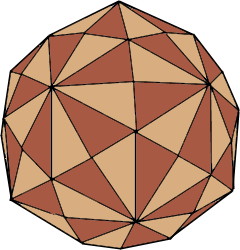
Der ultimative katalanische Körper mit 120 Dreiecksflächen.
Dual zum komplexesten archimedischen Körper.
|
|
Was ist ein Hexakisikosaeder?
Ein Hexakisikosaeder ist der ultimative katalanische Körper mit maximaler Komplexität:
- Definition: Polyeder mit 120 unregelmäßigen Dreiecksflächen
- Flächen: Jede Fläche ist ein skalenes Dreieck
- Dual: Zum Truncated Icosidodecahedron (62 Flächen)
- Ecken: 62 verschiedene Eckentypen
- Kanten: 180 Kanten in drei Längen
- Symmetrie: Ikosaedrische Symmetriegruppe
Geometrische Eigenschaften des Hexakisikosaeders
Das Hexakisikosaeder zeigt die ultimative geometrische Komplexität:
Ultimative Parameter
- Kantenlängen: Drei verschiedene Kantenlängen a, b, c
- Flächen: 120 kongruente skalene Dreiecke
- Euler-Charakteristik: V - E + F = 62 - 180 + 120 = 2
- Dualform: Truncated Icosidodecahedron
Ultimative Eigenschaften
- Höchste Komplexität: Katalanischer Körper mit den meisten Flächen
- Dreiecksflächen: Jede Fläche ist ein skalenes Dreieck
- Goldener Schnitt: Proportionen enthalten φ und √5
- Ikosaedrische Symmetrie: 120 Symmetrieoperationen
Mathematische Beziehungen
Das Hexakisikosaeder folgt den komplexesten mathematischen Gesetzen mit goldenem Schnitt:
Volumenformel
Höchst komplexe Formel mit verschachtelten Wurzeln. Koeffizient ≈ 13.36 aus ikosaedrischer Komplexität.
Oberflächenformel
Summe von 120 skalenen Dreiecken. Goldener Schnitt √5 in ultimativer Komplexität.
Anwendungen des Hexakisikosaeders
Hexakisikosaeder finden Anwendung in höchst spezialisierten Bereichen:
Spitzenforschung
- Komplexe Kristallographie und Quasikristalle
- Ultimative Molekülkäfig-Strukturen
- Mathematische Topologie-Extremfälle
- Höchst-Symmetriegruppen-Studien
Höchst-Technik
- Ultimative 3D-Modellierungs-Challenges
- Algorithmus-Stress-Tests für Extremgeometrien
- Präzisions-Kalibrierungs-Standards
- High-End-Visualisierungssysteme
Elite-Bildung
- Ultimative Geometrie-Herausforderungen
- Katalanische Körper Meisterklassen
- Dualitäts-Prinzipien auf höchstem Niveau
- Ikosaedrische Symmetrie-Expertise
Extreme Kunst
- Monumentale skulpturale Meisterwerke
- Ultimative mathematische Kunstformen
- Höchst-komplexe dekorative Systeme
- Avantgarde-Architektur-Extreme
Formeln für das Hexakisikosaeder
Oberfläche A
Ultimative Oberflächenformel mit goldenem Schnitt √5
Volumen V
Volumen mit höchst komplexen verschachtelten Wurzeln
Kantenradius RK
Kantenradius mit goldenem Schnitt
Innenradius RI
Innenradius mit ultimativer √5-Abhängigkeit
Dreiecks-Eigenschaften (Ultimative Komplexität)
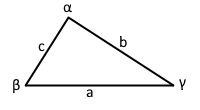
Grundparameter (längste)
b = 3a(4+√5)/22 ≈ 0.85a
c = 5a(7-√5)/44 ≈ 0.54a
Jedes der 120 skalenen Dreiecke hat diese drei Kantenlängen
Winkel im skalenen Dreieck
≈ 88° 59' 30"
≈ 58° 14' 17"
≈ 32° 46' 13"
Die charakteristischen Winkel jeder der 120 Dreiecksflächen
Berechnungsbeispiel für ein Hexakisikosaeder
Gegeben
Gesucht: Alle Eigenschaften des ultimativen katalanischen Körpers
1. Oberflächenberechnung
Die Oberfläche beträgt etwa 442 Flächeneinheiten
2. Volumenberechnung
Das Volumen beträgt etwa 855 Kubikeinheiten
3. Kantenlängen-Verhältnisse
Mittlere Kante: 3.40, Kurze Kante: 2.16 Einheiten
4. Radien
Kantenradius: 5.86, Innenradius: 5.80 Einheiten
5. Der Ultimative Katalanische Körper
Der ultimative katalanische Körper mit höchster mathematischer Raffinesse
Das Hexakisikosaeder: Der ultimative katalanische Körper
Das Hexakisikosaeder steht als der absolute Höhepunkt der katalanischen Körper-Familie und verkörpert die ultimative Synthese aus mathematischer Komplexität und geometrischer Perfektion. Mit seinen 120 skalenen Dreiecksflächen repräsentiert es die maximale Flächenanzahl, die bei einem katalanischen Körper erreicht werden kann, und stellt damit den Gipfel der polyhedral möglichen Komplexität dar. Als dualer Körper zum Truncated Icosidodecahedron - dem komplexesten aller archimedischen Körper - verkörpert es die tiefsten Geheimnisse der ikosaedrischen Symmetrie und des goldenen Schnitts in ihrer ultimativsten Form, wobei jede seiner 120 identischen Flächen ein perfektes skalenes Dreieck darstellt, das durch außerordentlich komplexe mathematische Beziehungen mit allen anderen Flächen verbunden ist.
Die ultimative Geometrie der 120 Dreiecksflächen
Das Hexakisikosaeder erreicht die absolute Spitze geometrischer Komplexität:
- 120 Dreiecksflächen: Maximale Flächenanzahl aller katalanischen Körper
- Skalene Dreiecke: Jede Fläche hat drei verschiedene Kantenlängen a, b, c
- Drei charakteristische Winkel: α ≈ 89°, β ≈ 58°, γ ≈ 33° in jedem Dreieck
- Ikosaedrische Vollsymmetrie: 120 Symmetrieoperationen der höchsten Ordnung
- Goldener Schnitt Dominanz: Alle Proportionen durchdrungen von φ und √5
- Ultimative Dualität: Jede Dreiecksfläche entspricht einer Ecke des 62-flächigen Duals
- Kantenlängen-Hierarchie: a : b : c im komplexen goldenen Verhältnis
Der Gipfel der katalanischen Tradition
Katalanische Vollendung
Als der komplexeste aller 13 katalanischen Körper verkörpert das Hexakisikosaeder die absolute Vollendung von Eugène Charles Catalans Vision uniformer polyhedral Dualität. Es zeigt, wie aus maximaler Ecken-Uniformität maximale Flächen-Komplexität entstehen kann.
Ultimative Dualität
Als Dual zum Truncated Icosidodecahedron (dem Gipfel der archimedischen Körper mit 62 Flächen) vertauscht es systematisch die ultimative Komplexität: 62 verschiedene Flächen werden zu 120 identischen Flächen bei 62 verschiedenen Eckentypen.
Ikosaedrische Suprematie
Mit der vollständigen ikosaedrischen Symmetriegruppe (120 Symmetrieoperationen) gehört es zu den symmetrischsten Objekten im dreidimensionalen Raum und verkörpert die höchste mögliche Ordnung in der Polyeder-Hierarchie.
Mathematische Ultimativität
Die Formeln erreichen den Gipfel der Komplexität mit mehrfach verschachtelten Wurzelausdrücken und goldenen Schnitt-Beziehungen, die die tiefsten Verbindungen zur pentagonalen Geometrie und zur Fibonacci-Folge offenbaren.
Der goldene Schnitt in ultimativer Perfektion
Das Hexakisikosaeder ist die ultimative Manifestation des goldenen Schnitts:
Ultimative Proportionen
Die drei Kantenlängen a, b, c stehen in hochkomplexen Verhältnissen zueinander, die alle vom goldenen Schnitt φ = (1+√5)/2 bestimmt werden. Diese Beziehungen sind so komplex, dass sie multiple √5-Terme und verschachtelte Brüche erfordern.
Formel-Suprematie
Alle geometrischen Formeln enthalten die komplexesten √5-Terme aller katalanischen Körper, was die fundamentale und ultimative Rolle der pentagonalen Geometrie in diesem Gipfel-Polyeder unterstreicht.
Winkel-Perfektion
Die drei charakteristischen Winkel α, β, γ jedes skalenen Dreiecks entstehen durch die komplexesten goldenen Schnitt-Konstruktionen und repräsentieren die ultimativen harmonischen Proportionen in der Geometrie.
Symmetrische Vollendung
Die 120-fache Wiederholung identischer skalener Dreiecke in perfekter ikosaedrischer Anordnung zeigt, wie der goldene Schnitt die ultimative dreidimensionale Harmonie erzeugen kann.
Wissenschaftliche Suprematie und kulturelle Bedeutung
Das Hexakisikosaeder findet Anwendung in den fortschrittlichsten Bereichen:
- Spitzen-Kristallographie: Modell für die komplexesten ikosaedrischen Kristallstrukturen und Quasikristalle
- Ultimative Molekularchemie: Template für die größten und komplexesten Molekülkäfige
- Mathematische Spitzenforschung: Studienobjekt für ultimative Symmetriegruppen und Topologie
- Geometrische Meisterkunst: Inspiration für die anspruchsvollsten skulpturalen Werke
- Elite-Bildung: Demonstration ultimativer Dualitätsprinzipien und Symmetriekonzepte
- Spitzen-Computergrafik: Ultimativer Benchmark für 3D-Modellierungsalgorithmen
- Philosophie der Vollendung: Symbol für die ultimative Harmonie zwischen Komplexität und Ordnung
Konstruktive Herausforderungen auf höchstem Niveau
Ultimative Präzision
Die Herstellung eines perfekten Hexakisikosaeders erfordert die höchste jemals erreichte Präzision bei der Fertigung der 120 skalenen Dreiecke. Jede Fläche muss drei exakte Kantenlängen und drei exakte Winkel aufweisen, die durch höchst irrationale Zahlen definiert sind.
Mathematische Suprematie
Die Berechnungen erfordern die komplexesten verschachtelten Wurzelausdrücke und transzendenten Funktionen aller geometrischen Objekte, was diesen Körper zum rechnerisch anspruchsvollsten Polyeder der Mathematik macht.
Technologische Grenzen
Selbst mit modernster CAD-Software und Präzisions-CNC-Fertigung ist es kaum möglich, physische Modelle mit der erforderlichen Genauigkeit herzustellen, um die theoretische Perfektion auch nur annähernd zu realisieren.
Qualitäts-Suprematie
Die Verifikation der geometrischen Korrektheit erfordert die fortschrittlichsten Messverfahren und computergestützten Analysesysteme, da selbst molekulare Abweichungen die ultimative Symmetrie zerstören können.
Philosophische und ästhetische Vollendung
Ultimative Harmonie
Das Hexakisikosaeder verkörpert die ultimative Harmonie zwischen Einfachheit (identische skalene Dreiecke) und Komplexität (120-fache Anordnung in ikosaedrischer Vollsymmetrie), was es zum philosophischen Symbol für höchste Vollendung macht.
Naturgesetze der Schönheit
Die auf dem goldenen Schnitt basierenden ultimativen Proportionen verleihen diesem Körper eine übernatürliche Schönheit, die sowohl mathematisch als höchste Vollendung begründbar als auch ästhetisch als Gipfel der Harmonie erfahrbar ist.
Ultimativer Bildungswert
Als ultimatives Demonstrationsobjekt für Dualität, Symmetrie und komplexe geometrische Beziehungen bietet es unübertroffene Möglichkeiten für den höchsten Mathematikunterricht und die wissenschaftliche Spitzenausbildung.
Kulturelle Vollendung
In allen Kulturen wird diese ultimative geometrische Form mit höchster Vollendung, spiritueller Transzendenz und der Erreichung mathematischer Perfektion assoziiert, was ihm eine universelle symbolische Bedeutung verleiht.
Zusammenfassung
Das Hexakisikosaeder steht als der absolute Gipfel aller katalanischen Körper und als der ultimative Ausdruck polyhedral möglicher Komplexität da. Seine 120 skalenen Dreiecksflächen, durchdrungen vom goldenen Schnitt in seiner komplexesten Form und arrangiert in perfekter ikosaedrischer Vollsymmetrie, machen es zum ultimativen Meisterwerk der Geometrie. Von seiner Entdeckung als dualer Körper zum komplexesten archimedischen Körper bis zu seinen Anwendungen in der Spitzenforschung zeigt es, wie mathematische Komplexität und ästhetische Schönheit ihre ultimative Vollendung erreichen können. Als Bindeglied zwischen der antiken Tradition der platonischen Körper und den modernsten Herausforderungen der computational geometry bleibt es der faszinierendste und herausforderndste Gegenstand für Spitzenforscher, Meisterkünstler und alle, die von der ultimativen Macht der Mathematik zur Erschaffung vollkommenster Formen begeistert sind.