Tetrakishexaeder Rechner
Rechner und Formeln zur Berechnung eines Tetrakishexaeder (Pyramidenwürfel)
Tetrakishexaeder Rechner
Das Tetrakishexaeder
Ein Tetrakishexaeder ist ein katalanischer Körper mit 24 gleichschenkligen Dreiecksflächen - dual zum Abgeschrägten Würfel.
Tetrakishexaeder Eigenschaften
Der Pyramiden-Würfel: Dual zum Abgeschrägten Würfel
Tetrakishexaeder Struktur
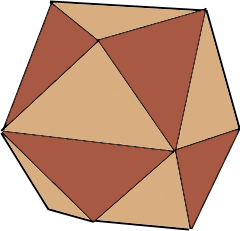
Der Pyramiden-Würfel mit 24 Dreiecksflächen.
Dual zum Abgeschrägten Würfel.
|
|
Was ist ein Tetrakishexaeder?
Ein Tetrakishexaeder ist ein faszinierender katalanischer Körper mit pyramidaler Struktur:
- Definition: Polyeder mit 24 gleichschenkligen Dreiecksflächen
- Flächen: Jede Fläche ist ein gleichschenkliges Dreieck
- Dual: Zum Abgeschrägten Würfel (14 Flächen)
- Ecken: 14 Ecken in zwei Typen
- Kanten: 36 Kanten in zwei Längen
- Struktur: Würfel mit 6 vierseitigen Pyramiden
Geometrische Eigenschaften des Tetrakishexaeders
Das Tetrakishexaeder zeigt bemerkenswerte pyramidale Eigenschaften:
Pyramidale Parameter
- Kantenlängen: Würfelkante (a) und Pyramidenkante (b = 3a/4)
- Flächen: 24 kongruente gleichschenklige Dreiecke
- Euler-Charakteristik: V - E + F = 14 - 36 + 24 = 2
- Dualform: Abgeschrägter Würfel
Pyramiden-Eigenschaften
- Katalanischer Körper: Dual zu uniformem Polyeder
- Dreiecksflächen: Jede Fläche ist ein gleichschenkliges Dreieck
- Kubische Basis: Grundstruktur basiert auf einem Würfel
- Pyramidenstruktur: 6 vierseitige Pyramiden auf Würfelflächen
Mathematische Beziehungen
Das Tetrakishexaeder folgt den eleganten mathematischen Gesetzen pyramidaler Geometrie:
Einfaches Volumen
Elegante Formel ohne Wurzeln. Koeffizient 1.5 aus pyramidaler Geometrie.
Dreiecks-Oberfläche
Summe von 24 gleichschenkligen Dreiecken. √5 in pyramidaler Form.
Anwendungen des Tetrakishexaeders
Tetrakishexaeder finden Anwendung in pyramidalen Strukturen:
Wissenschaft & Forschung
- Kubische Kristallstrukturen mit Pyramidenerweiterungen
- Oberflächenerweiterung kubischer Grundformen
- Geometrische Transformationsstudien
- Dual-Polyeder Forschung
Technik & Design
- 3D-Modellierung pyramidaler Formen
- Algorithmus-Tests für Dreiecks-Geometrien
- Architektonische Pyramiden-Elemente
- Oberflächenerweiterung von Würfeln
Bildung & Lehre
- Pyramidale Geometrie Demonstrationen
- Katalanische Körper mit Dreiecken
- Dualitäts-Prinzipien bei Würfeln
- Oberflächenerweiterung Studien
Kunst & Gestaltung
- Pyramidale Skulpturen und Installationen
- Dreiecks-basierte Muster und Ornamente
- Kubisch-pyramidale Designs
- Architektonische Pyramiden-Motive
Formeln für das Tetrakishexaeder
Oberfläche A
Oberfläche mit √5 aus pyramidaler Geometrie
Volumen V
Volumen mit einfachen Beziehungen
Kantenradius RK
Kantenradius mit √2
Innenradius RI
Innenradius mit √5-Abhängigkeit
Pyramiden-Eigenschaften (Kubische Basis)
Grundparameter (Würfelbasis)
b = 3a/4 = 0.75a
h = 3a/2 = 1.5a
Jedes der 24 gleichschenkligen Dreiecke hat kubisch-pyramidale Proportionen
Kubisch-Pyramidale Eigenschaften
6 vierseitige Pyramiden auf Würfelflächen
Dual zum abgeschrägten Würfel
Charakteristische √2- und √5-Beziehungen der kubisch-pyramidalen Geometrie
Berechnungsbeispiel für ein Tetrakishexaeder
Gegeben
Gesucht: Alle Eigenschaften des Pyramiden-Würfels
1. Oberflächenberechnung
Die Oberfläche beträgt etwa 107 Flächeneinheiten
2. Volumenberechnung
Das Volumen beträgt genau 96 Kubikeinheiten
3. Pyramidenkante und Höhe
Pyramidenkante: 3.0, Höhe: 6.0 Einheiten
4. Radien
Kantenradius: 2.83, Innenradius: 2.68 Einheiten
5. Der Pyramiden-Würfel
Der kubisch-pyramidale Dreieckskörper mit eleganter Symmetrie
Das Tetrakishexaeder: Der kubisch-pyramidale Katalanische Körper
Das Tetrakishexaeder, auch als Pyramidenwürfel bekannt, ist ein faszinierender katalanischer Körper, der die elegante Synthese aus kubischer Grundstruktur und pyramidaler Oberflächenerweiterung verkörpert. Mit seinen 24 gleichschenkligen Dreiecksflächen stellt es ein bemerkenswertes Beispiel dafür dar, wie aus einer einfachen geometrischen Grundform - dem Würfel - durch systematische Erweiterung eine komplexe und ästhetisch ansprechende dreidimensionale Struktur entstehen kann. Als dualer Körper zum abgeschrägten Würfel zeigt es die tiefe Verbindung zwischen uniformen Polyedern und ihren katalanischen Partnern und demonstriert, wie mathematische Dualität zu völlig neuen geometrischen Formen führen kann. Seine charakteristische Struktur aus sechs vierseitigen Pyramiden, die auf die Flächen eines zentralen Würfels aufgesetzt sind, macht es zu einem idealen Studienobjekt für das Verständnis pyramidaler Geometrie und Oberflächenerweiterung.
Die kubisch-pyramidale Harmonie der 24 Dreiecksflächen
Das Tetrakishexaeder fasziniert durch seine pyramidale Perfektion:
- 24 Dreiecksflächen: Jede Fläche ist ein gleichschenkliges Dreieck mit spezifischen Proportionen
- Pyramidale Struktur: Sechs vierseitige Pyramiden auf den Flächen eines zentralen Würfels
- Zwei Kantenlängen: Würfelkante (a) und Pyramidenkante (b = 3a/4)
- Kompakte Struktur: 14 Ecken in optimaler kubisch-pyramidaler Anordnung
- Einfache Geometrie: Klare Beziehungen ohne komplexe irrationale Zahlen
- Perfekte Integration: Die 24 Dreiecke fügen sich harmonisch zusammen
- Dualitätsprinzip: Jede Dreiecksfläche entspricht einer Ecke des abgeschrägten Würfels
Katalanische Tradition und kubisch-pyramidale Dualität
Katalanische Klarheit
Als einer der verständlichsten katalanischen Körper zeigt das Tetrakishexaeder die Schönheit der Dualität zwischen uniformen Polyedern und ihren triangulären Partnern. Die kubische Basis verleiht ihm besondere Klarheit und Zugänglichkeit.
Kubisch-Pyramidale Dualität
Als Dual zum abgeschrägten Würfel mit 14 verschiedenen Flächen (6 Achtecke + 8 Dreiecke) vertauscht es systematisch Flächenvielfalt mit dreieckiger Homogenität, wobei die kubische Symmetrie die harmonischen Beziehungen verstärkt.
Geometrische Zugänglichkeit
Mit 24 Flächen erreicht es eine ideale Balance zwischen Komplexität und Verständlichkeit, die es zu einem perfekten Studienobjekt für kubische Erweiterung und pyramidale Geometrie macht.
Mathematische Einfachheit
Die Formeln zeigen klare Beziehungen mit einfachen Koeffizienten und nur √2 und √5, was das Verständnis der zugrundeliegenden kubisch-pyramidalen Geometrie erleichtert und fördert.
Die einfache Geometrie der kubischen Erweiterung
Das Tetrakishexaeder basiert auf klaren geometrischen Prinzipien:
Kubische Erweiterung
Die Struktur entsteht durch das Aufsetzen von sechs vierseitigen Pyramiden auf die Flächen eines Würfels. Die Pyramidenhöhen und -kantenlängen folgen einfachen Verhältnissen zur Würfelkante, was die Konstruktion besonders elegant macht.
Einfache Formeln
Alle geometrischen Formeln sind bemerkenswert einfach: Das Volumen ist genau 1.5a³, die Höhe ist 1.5a, und die Pyramidenkante ist 0.75a - klare Verhältnisse ohne komplexe irrationale Zahlen.
Pyramidale Harmonie
Die Anordnung der 24 Dreiecksflächen folgt den Gesetzen der kubischen Symmetrie, wodurch jede Fläche in perfekter Harmonie mit allen anderen steht und eine bemerkenswerte strukturelle Einheit entsteht.
Konstruktive Klarheit
Die kubisch-pyramidale Organisation ermöglicht eine intuitive Konstruktion und einfache Visualisierung, was es zu einem idealen Einstiegsobjekt für das Studium katalanischer Körper macht.
Wissenschaftliche und praktische Bedeutung
Das Tetrakishexaeder findet Anwendung in verschiedenen Bereichen:
- Kristallographie: Modell für kubische Kristallstrukturen mit pyramidalen Erweiterungen
- Oberflächenerweiterung: Paradigma für die systematische Erweiterung kubischer Grundformen
- Architektur: Inspiration für kubisch-pyramidale Strukturen und Oberflächengestaltung
- Materialwissenschaft: Template für strukturierte Oberflächen und Beschichtungen
- Bildung: Ideales Demonstrationsobjekt für Dualität und pyramidale Geometrie
- 3D-Modellierung: Einfaches Referenzobjekt für triangulierte Oberflächen
- Ingenieurswesen: Modell für verstärkte kubische Strukturen
Konstruktion und pyramidale Präzision
Einfache Konstruktion
Die Herstellung ist bemerkenswert einfach: Sechs identische vierseitige Pyramiden werden auf die Flächen eines Würfels aufgesetzt. Die klaren Proportionsverhältnisse erleichtern die präzise Fertigung erheblich.
Fertigungsvorteile
Die kubische Grundstruktur und die einfachen Verhältnisse (3:4 für Pyramidenkante, 3:2 für Höhe) machen die Fertigung besonders zugänglich und kostengünstig, da keine komplexen irrationalen Proportionen erforderlich sind.
Qualitätskontrolle
Die Überprüfung der kubisch-pyramidalen Proportionen kann systematisch erfolgen, was die Qualitätssicherung vereinfacht und eine zuverlässige Produktion ermöglicht.
Moderne Fertigung
CNC-Maschinen und 3D-Drucker können die einfachen Verhältnisse perfekt umsetzen, wodurch hochwertige physische Modelle für Forschung und Bildung kostengünstig realisierbar werden.
Ästhetische und pädagogische Dimensionen
Kubisch-Pyramidale Ästhetik
Die Kombination aus kubischer Ordnung und pyramidaler Dynamik erzeugt eine einzigartige ästhetische Wirkung, die sowohl strukturelle Stabilität als auch aufstrebende Energie ausstrahlt.
Pädagogischer Wert
Als einer der zugänglichsten katalanischen Körper ist es ideal geeignet, um Studenten die Grundprinzipien der Dualität, Oberflächenerweiterung und pyramidalen Geometrie näherzubringen.
Symbolische Bedeutung
In der Designphilosophie symbolisiert es die harmonische Verbindung zwischen fundamentaler Struktur und dynamischer Erweiterung, zwischen Stabilität und Wachstum.
Kulturelle Relevanz
Als Vertreter der kubisch-pyramidalen Familie geometrischer Formen verbindet es sich mit kulturellen Traditionen, die sowohl strukturelle Solidität als auch spirituelle Aspiration schätzen.
Zusammenfassung
Das Tetrakishexaeder verkörpert die elegante Einfachheit der katalanischen Körper-Familie. Mit seinen 24 gleichschenkligen Dreiecksflächen, die in perfekter kubisch-pyramidaler Symmetrie angeordnet sind, zeigt es, wie mathematische Prinzipien geometrische Schönheit von bemerkenswerter Klarheit und Zugänglichkeit erzeugen können. Die durchgängig einfachen Proportionsverhältnisse verbinden es tief mit der praktischen Geometrie und machen es zu einem idealen Studienobjekt für die Erforschung von Dualität, Oberflächenerweiterung und den fundamentalen Prinzipien der dreidimensionalen Konstruktion. Von seiner theoretischen Bedeutung in der reinen Mathematik bis zu seinen praktischen Anwendungen in Kristallographie und Architektur bleibt das Tetrakishexaeder ein faszinierendes Beispiel dafür, wie elegante mathematische Strukturen sowohl intellektuelle Befriedigung als auch praktischen Nutzen bieten können.