Frequency and Wavelengths

Calculator and formulas for calculating frequency and wavelength

Frequency / Wavelength Calculator

Frequency-Wavelength Calculator

On this page you can calculate the wavelength for a given frequency, or the frequency for a given wavelength. Wavelengths for electrical oscillations, light, and sound can be calculated.

What should be calculated?

Calculate wavelength λ

Calculate frequency f

Medium / Wave type

Frequency f

Wavelength λ

Decimal places

Result

Wavelength:

Frequency:

Frequency & Wavelength

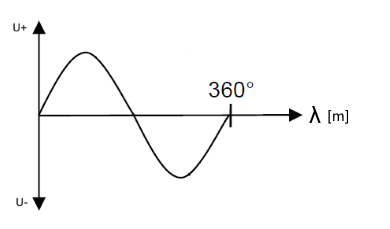
Wavelength λ of a periodic oscillation

Parameters

\(\displaystyle \lambda\) = Wavelength [m]

\(\displaystyle f\) = Frequency [Hz]

\(\displaystyle c\) = Propagation speed [m/s]

Basic formulas

\[\lambda = \frac{c}{f}\]

\[f = \frac{c}{\lambda}\]

Tip

A calculator for calculating frequency and period can be found here.

Propagation speeds

Speeds of different types of waves

The wavelength depends on the frequency and the propagation speed of the waves. The following table shows the propagation speed of different waves in various media.

Electromagnetic waves

Free space (vacuum):

299,792,458 km/s

Electrical conductors:

≈ 240,000 km/s

Copper PCBs:

≈ 200,000 km/s

Light waves:

299,792,458 km/s

Mechanical waves

Sound in air (+20°C):

343 m/s

Sound in water:

1,470 m/s

Sound in steel:

≈ 5,000 m/s

Seismic waves:

1-14 km/s

Example calculations

Practical calculation examples

Example 1: Calculating frequency

Given: λ = 10m, c = 300 m/s (example sound speed)

\[f = \frac{c}{\lambda} = \frac{300 \text{ m/s}}{10 \text{ m}} = 30 \text{ Hz}\]

Low-frequency sound wave

Example 2: Calculating wavelength

Given: f = 50Hz, c = 340 m/s (sound speed in air)

\[\lambda = \frac{c}{f} = \frac{340 \text{ m/s}}{50 \text{ Hz}} = 6.8 \text{ m}\]

Low-frequency sound wave in air

Example 3: Electromagnetic wave

Given: f = 100MHz (FM radio), c = 3×10⁸ m/s

\[\lambda = \frac{3 \times 10^8 \text{ m/s}}{100 \times 10^6 \text{ Hz}} = 3 \text{ m}\]

FM radio frequency with 3m wavelength

Wavelength spectrum

Radio waves:

Long wave: 1-10 km

Medium wave: 100-1000 m

Short wave: 10-100 m

FM: 1-10 m

Microwaves:

WLAN 2.4GHz: 12.5 cm

WLAN 5GHz: 6 cm

Radar: 1-30 cm

Microwave: 12.2 cm

Light:

Infrared: 0.7-1000 µm

Visible: 380-780 nm

Ultraviolet: 10-380 nm

X-ray: 0.01-10 nm

Formulas for Frequency and Wavelength

Basics of wave propagation

The wavelength refers to the length of one period of a propagating oscillation. It depends on the frequency and the propagation speed of the waves.

Basic relationships

The wavelength λ in meters is calculated by dividing the propagation speed c by the frequency f.

Wavelength formula

\[\lambda = \frac{c}{f}\]

The wavelength is proportional to the speed and inversely proportional to the frequency.

This results in the following formula for calculating the frequency:

Frequency formula

\[f = \frac{c}{\lambda}\]

The frequency is proportional to the speed and inversely proportional to the wavelength.

Different types of waves

Electromagnetic waves

Propagation: In vacuum at the speed of light
Medium: Do not require a transmission medium
Speed: c = 299,792,458 m/s
Spectrum: Radio to gamma radiation

Mechanical waves

Propagation: Require a medium
Medium: Air, water, solids
Speed: Depends on material
Examples: Sound, seismics, water waves

Practical applications

Radio technology

Antenna design
Frequency bands
Propagation models
Interference analysis

Optics

Color spectrum
Diffraction grating
Laser technology
Spectroscopy

Acoustics

Room acoustics
Ultrasound
Musical instruments
Noise protection

Legend

Symbol definitions

λ (Lambda): Wavelength in meters [m]

f: Frequency in hertz [Hz]

c: Propagation speed [m/s]

T: Period duration in seconds [s]

ω: Angular frequency [rad/s]

k: Wave number [1/m]

Design notes

Practical considerations

Antenna design: Optimum length at λ/4, λ/2 or multiples
Wave propagation: Obstacles can cause diffraction at λ size
Interference: Constructive/destructive superposition at λ/2 distances
Resonance: Cavity resonators at λ/2 dimensions
Dispersion: Speed can be frequency dependent
Attenuation: Losses often depend on frequency and medium

AC functions