Schräger Zylinder Rechner
Rechner und Formeln zur Berechnung eines schrägen Zylinders
Schräger Zylinder Rechner
Der schräge Zylinder
Der schräge Zylinder ist ein geneigter Kreiszylinder mit abgeschrägten Endflächen.
Schräger Zylinder Eigenschaften
Der schräge Zylinder: Geneigter Kreiszylinder mit abgeschrägten Endflächen
Schräger Zylinder Visualisierung
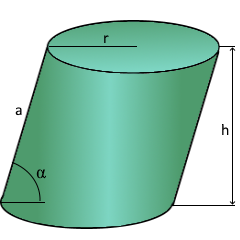
Schräger Zylinder
Geneigter Zylinder mit Winkel α
Parameter
r: Radius der Grundfläche
α: Neigungswinkel
h: Lotrechte Höhe
a: Seitenlänge (schräg)
Geneigter Kreiszylinder.
Trigonometrische Beziehungen.
|
|
Was ist ein schräger Zylinder?
Der schräge Zylinder ist ein wichtiger geometrischer Körper:
- Definition: Kreiszylinder mit zur Basis geneigter Seitenfläche
- Neigungswinkel α: Winkel zwischen Seitenlinie und Basis
- Eigenschaften: Elliptische Schnittflächen bei schrägen Schnitten
- Unterscheidung: Höhe h (lotrecht) vs. Seitenlänge a (schräg)
- Anwendung: Architektur, Maschinenbau, schräge Rohrleitungen
- Mathematik: Trigonometrische Beziehungen h = a·sin(α)
Geometrische Eigenschaften des schrägen Zylinders
Der schräge Zylinder zeigt charakteristische geometrische Eigenschaften:
Grundparameter
- Radius r: Radius der kreisförmigen Grundfläche
- Neigungswinkel α: Winkel der Seitenlinie zur Basis
- Höhe h: Lotrechter Abstand zwischen den Grundflächen
- Seitenlänge a: Schräge Länge der Mantellinie
Besondere Eigenschaften
- Parallelschnitte: Alle Parallelschnitte sind kongruente Kreise
- Schräge Schnitte: Ergeben elliptische Querschnitte
- Gleiches Volumen: Wie senkrechter Zylinder gleicher Grundfläche und Höhe
- Trigonometrie: h = a·sin(α), a = h/sin(α)
Mathematische Beziehungen des schrägen Zylinders
Der schräge Zylinder folgt eleganten trigonometrischen Gesetzen:
Volumen-Formel
Das Volumen ist identisch mit einem senkrechten Zylinder. Cavalieri-Prinzip!
Trigonometrische Beziehung
Fundamentale trigonometrische Beziehung zwischen Höhe, Seitenlänge und Neigungswinkel.
Anwendungen des schrägen Zylinders
Schräge Zylinder finden Anwendung in verschiedenen Bereichen:
Architektur & Bauwesen
- Schräge Säulen und Stützen
- Geneigte Rohrleitungen
- Architektonische Elemente
- Schrägaufzüge und Rampen
Maschinenbau & Technik
- Schrägbohrungen
- Geneigte Zylinder in Motoren
- Hydraulische Komponenten
- Förderanlagen und Rutschen
Verfahrenstechnik
- Schräge Reaktoren
- Geneigte Mischbehälter
- Abfüllvorrichtungen
- Separationsanlagen
Fahrzeugtechnik
- Schrägmotoren (V-Motoren)
- Geneigte Auspuffrohre
- Hydraulikzylinder
- Federungselemente
Formeln zum schrägen Zylinder
Höhe (h)
Lotrechte Höhe aus Seitenlänge und Winkel
Seitenlänge (a)
Schräge Seitenlänge aus Höhe und Winkel
Volumen (V)
Volumen wie beim senkrechten Zylinder
Seitenfläche (L)
Mantelfläche mit schräger Seitenlänge
Weitere Formeln
\[A = \pi r^2\]
\[P = 2\pi r\]
\[S = 2A + L\]
\[\cot(\alpha) = \frac{\sqrt{a^2-h^2}}{h}\]
Der schräge Zylinder verbindet Geometrie mit Trigonometrie
Berechnungsbeispiel für einen schrägen Zylinder
Gegeben
Gesucht: Alle Parameter des schrägen Zylinders
1. Seitenlängen-Berechnung
Für h = 8 cm, α = 20°:
\[a = \frac{h}{\sin(\alpha)}\] \[a = \frac{8}{\sin(20°)}\] \[a = \frac{8}{0.342} ≈ 23.39 \text{ cm}\]Die schräge Seitenlänge beträgt etwa 23.39 cm
2. Volumen-Berechnung
Für r = 3 cm, h = 8 cm:
\[V = \pi r^2 h\] \[V = \pi \cdot 3^2 \cdot 8\] \[V = \pi \cdot 9 \cdot 8 = 72\pi\] \[V ≈ 226.19 \text{ cm}^3\]Das Volumen beträgt etwa 226.19 cm³
3. Basisfläche und Umfang
Grundfläche und Umfang:
\[A = \pi r^2 = \pi \cdot 9 ≈ 28.27 \text{ cm}^2\] \[P = 2\pi r = 2\pi \cdot 3 = 6\pi ≈ 18.85 \text{ cm}\]Basisfläche ≈ 28.27 cm², Umfang ≈ 18.85 cm
4. Oberflächen-Berechnung
Mantelfläche und Gesamtoberfläche:
\[L = 2\pi r a = 2\pi \cdot 3 \cdot 23.39\] \[L ≈ 441.07 \text{ cm}^2\] \[S = 2A + L = 2 \cdot 28.27 + 441.07\] \[S ≈ 497.61 \text{ cm}^2\]Die Gesamtoberfläche beträgt etwa 497.61 cm²
5. Trigonometrische Kontrolle
h = a·sin(α) = 23.39·sin(20°) ≈ 8.00 cm ✓
b = a·cos(20°) ≈ 21.97 cm
a² = h² + b² ✓
Alle trigonometrischen Beziehungen sind erfüllt
6. Zusammenfassung
Der schräge Zylinder mit allen charakteristischen Parametern
7. Praktisches Beispiel: Schräge Säule
Geneigte Säule
20° Neigung
S ≈ 497.61 cm²
Oberfläche
Gleiches Volumen
wie senkrechte Säule
Eine schräge Säule bietet architektonische Eleganz bei gleicher Tragfähigkeit
8. Vergleich mit senkrechtem Zylinder
r=3, h=8, α=20°
V≈226.19 cm³
r=3, h=8
V≈226.19 cm³
Gleiches Volumen!
Cavalieri-Prinzip
Das Volumen ist bei gleicher Grundfläche und Höhe identisch - ein Triumph der Geometrie!
Der schräge Zylinder: Trigonometrie trifft Geometrie
Der schräge Zylinder ist ein faszinierender geometrischer Körper, der die Eleganz der Trigonometrie mit der Praktikabilität der Zylindergeometrie verbindet. Als geneigter Kreiszylinder mit abgeschrägten Endflächen behält er alle wesentlichen Eigenschaften des klassischen Zylinders, erweitert sie aber um die Komplexität trigonometrischer Beziehungen. Diese einzigartige Kombination macht ihn zu einem wichtigen Element in Architektur, Maschinenbau und allen Bereichen, wo Neigungen und schräge Konstruktionen eine Rolle spielen.
Die Geometrie der Neigung
Der schräge Zylinder zeigt die Perfektion geneigter Geometrie:
- Neigungswinkel α: Bestimmt die Schrägstellung der Mantelfläche
- Höhe vs. Seitenlänge: h = a·sin(α) - fundamentale trigonometrische Beziehung
- Gleiches Volumen: Cavalieri-Prinzip - identisch mit senkrechtem Zylinder
- Elliptische Schnitte: Schräge Schnitte ergeben Ellipsen statt Kreise
- Parallelschnitte: Alle zur Basis parallelen Schnitte bleiben kreisförmig
- Trigonometrische Eleganz: Sinus, Cosinus und Tangens in perfekter Harmonie
- Praktische Vielseitigkeit: Lösungen für reale Konstruktionsprobleme
Vielseitige Anwendungen
Architektonische Innovation
Schräge Säulen und geneigte Stützen schaffen dynamische Architektur und ermöglichen innovative Tragwerkslösungen bei gleichbleibender Stabilität.
Maschinenbau-Präzision
In der Technik ermöglichen schräge Zylinder optimierte Konstruktionen für Hydraulik, Motorbau und Förderanlagen mit exakten trigonometrischen Berechnungen.
Verfahrenstechnische Effizienz
Geneigte Reaktoren und Mischbehälter nutzen die Schwerkraft optimal und verbessern Durchmischung und Prozessführung durch kontrollierte Neigung.
Fahrzeugtechnische Perfektion
V-Motoren und schrägstehende Zylinder maximieren Leistung bei minimalem Bauraum und zeigen die praktische Eleganz geneigter Geometrie.
Zusammenfassung
Der schräge Zylinder verkörpert die perfekte Synthese aus trigonometrischer Präzision und geometrischer Funktionalität. Seine durch den Neigungswinkel α charakterisierte Form, beschrieben durch die elegante Beziehung h = a·sin(α), macht ihn zu einem der vielseitigsten und praktischsten geometrischen Körper. Das faszinierende Cavalieri-Prinzip zeigt, dass das Volumen trotz der Neigung identisch mit einem senkrechten Zylinder bleibt - ein Triumph der mathematischen Logik. Von dynamischen Architekturelementen über präzise Maschinenbauteile bis hin zu effizienten Verfahrensanlagen - der schräge Zylinder beweist, dass Neigung nicht Komplikation, sondern Innovation bedeutet. Er ist der lebende Beweis dafür, dass Trigonometrie nicht nur abstrakte Schönheit besitzt, sondern konkrete Lösungen für komplexe Konstruktionsaufgaben bietet und dabei zeigt, wie mathematische Eleganz praktische Probleme elegant löst.
|
|
|
|