Zylinder Rechner
Rechner und Formeln zur Berechnung der Parameter eines Zylinders
Zylinder Rechner
Der Kreiszylinder
Der Zylinder ist ein rotationssymmetrischer Körper mit kreisförmiger Grundfläche.
Zylinder Eigenschaften
Der Kreiszylinder: Rotationssymmetrischer Körper mit kreisförmiger Grundfläche
Zylinder Visualisierung
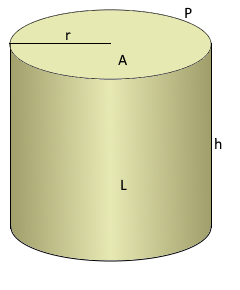
Kreiszylinder
Rotationssymmetrischer Grundkörper
Parameter
r: Radius der Grundfläche
h: Höhe des Zylinders
A: Kreisförmige Basisfläche
L: Rechteckige Mantelfläche
Rotationssymmetrischer Körper.
Kreisförmige Grund- und Deckfläche.
|
|
Was ist ein Zylinder?
Der Kreiszylinder ist einer der wichtigsten geometrischen Grundkörper:
- Definition: Rotationssymmetrischer Körper mit kreisförmiger Grundfläche
- Eigenschaften: Zwei parallele Kreisflächen als Grund- und Deckfläche
- Mantelfläche: Rechteckige Fläche bei Abwicklung des Zylinders
- Rotation: Entsteht durch Rotation eines Rechtecks um eine Seite
- Anwendung: Behälterbau, Maschinenbau, Architektur, Technik
- Mathematik: Grundlage für viele weitere geometrische Körper
Geometrische Eigenschaften des Zylinders
Der Kreiszylinder zeigt charakteristische geometrische Eigenschaften:
Grundparameter
- Radius r: Radius der kreisförmigen Grundfläche
- Höhe h: Abstand zwischen Grund- und Deckfläche
- Durchmesser d: d = 2r (Durchmesser der Grundfläche)
- Achse: Gerade Linie durch die Mittelpunkte der Kreisflächen
Besondere Eigenschaften
- Rotationssymmetrie: Unendlich viele Symmetrieachsen
- Parallele Grundflächen: Kreis mit identischem Radius
- Mantelfläche: Abwickelbar zu einem Rechteck
- Volumen: Grundfläche mal Höhe (V = πr²h)
Mathematische Beziehungen des Zylinders
Der Kreiszylinder folgt fundamentalen mathematischen Gesetzen:
Volumen-Formel
Grundfläche mal Höhe. Fundamentales Volumenprinzip.
Oberflächen-Formel
Zwei Grundflächen plus Mantelfläche.
Anwendungen des Zylinders
Zylinder finden Anwendung in unzähligen Bereichen:
Behälterbau & Tankbau
- Druckbehälter und Lagertanks
- Silos für Schüttgut
- Reaktoren in der Verfahrenstechnik
- Wassertanks und Speicher
Maschinenbau & Automotive
- Motorzylinder und Kolben
- Hydraulikzylinder
- Wellen und Achsen
- Rohrleitungen
Architektur & Bauwesen
- Säulen und Stützen
- Rohrleitungsinstallationen
- Schornsteine und Türme
- Brückenpfeiler
Wissenschaft & Forschung
- Messzylinder und Laborgeräte
- Optische Linsen und Prismen
- Elektronenröhren
- Forschungsreaktoren
Formeln zum Kreiszylinder
Volumen (V)
Grundfläche mal Höhe
Grundfläche (A)
Kreisförmige Basisfläche
Mantelfläche (L)
Umfang mal Höhe
Umfang (P)
Umfang der Grundfläche
Gesamtoberfläche (S)
Zwei Grundflächen plus Mantelfläche
Weitere Parameter
\[d = 2r\]
\[r = \frac{P}{2\pi}\]
\[h = \frac{V}{\pi r^2}\]
\[s = h\] (gerade)
Der Kreiszylinder als fundamentaler geometrischer Grundkörper
Berechnungsbeispiel für einen Kreiszylinder
Gegeben
Gesucht: Alle Parameter des Kreiszylinders
1. Grundfläche berechnen
Für r = 5 cm:
\[A = \pi r^2\] \[A = \pi \cdot 5^2 = 25\pi\] \[A ≈ 78.54 \text{ cm}^2\]Die Grundfläche beträgt etwa 78.54 cm²
2. Umfang berechnen
Umfang der Grundfläche:
\[P = 2\pi r\] \[P = 2\pi \cdot 5 = 10\pi\] \[P ≈ 31.42 \text{ cm}\]Der Umfang beträgt etwa 31.42 cm
3. Mantelfläche berechnen
Rechteckige Mantelfläche:
\[L = 2\pi r h\] \[L = P \cdot h = 10\pi \cdot 12\] \[L = 120\pi ≈ 377.00 \text{ cm}^2\]Die Mantelfläche beträgt etwa 377.00 cm²
4. Volumen berechnen
Volumen des Zylinders:
\[V = \pi r^2 h\] \[V = A \cdot h = 25\pi \cdot 12\] \[V = 300\pi ≈ 942.48 \text{ cm}^3\]Das Volumen beträgt etwa 942.48 cm³
5. Gesamtoberfläche berechnen
Summe aller Teilflächen:
\[S = 2A + L\] \[S = 2 \cdot 78.54 + 377.00\] \[S = 157.08 + 377.00 = 534.08 \text{ cm}^2\]Die Gesamtoberfläche beträgt etwa 534.08 cm²
6. Geometrische Analyse
d = 2r = 10 cm
h/d = 12/10 = 1.2
Schlanker Zylinder
Ein schlanker Zylinder mit Höhe größer als Durchmesser
7. Zusammenfassung
Der Kreiszylinder mit allen charakteristischen Parametern
8. Praktisches Beispiel: Lagertank
V ≈ 942.48 cm³
≈ 0.94 Liter
S ≈ 534.08 cm²
Blechverbrauch
Schlanke Bauform
Stabile Konstruktion
Ein Lagertank mit optimaler Höhe-Durchmesser-Relation
9. Alternative Proportionen
r=10, h=6
V≈1884.96 cm³
r≈5.64, h=10
V≈1000 cm³
r=3, h=20
V≈565.49 cm³
Verschiedene Proportionen für unterschiedliche Anwendungszwecke
Der Kreiszylinder: Vollendung der geometrischen Perfektion
Der Kreiszylinder ist einer der fundamentalsten und elegantesten geometrischen Körper, der die Perfektion kreisförmiger Symmetrie mit der Praktikabilität dreidimensionaler Formen verbindet. Als rotationssymmetrischer Körper mit kreisförmiger Grundfläche vereint er in sich die mathematische Klarheit einfacher Formeln mit der technischen Anwendbarkeit in unzähligen Bereichen der Technik, Wissenschaft und des täglichen Lebens. Diese einzigartige Kombination aus geometrischer Einfachheit und praktischer Vielseitigkeit macht ihn zum unverzichtbaren Grundkörper der modernen Ingenieurstechnik.
Die Geometrie der Rotation
Der Kreiszylinder zeigt die Perfektion rotationssymmetrischer Geometrie:
- Rotationsentstehung: Rotation eines Rechtecks um eine seiner Seiten
- Kreisförmige Grundflächen: A = πr² als perfekte geometrische Form
- Rechteckige Mantelfläche: L = 2πrh bei Abwicklung des Zylinders
- Volumenformel V = πr²h: Grundfläche mal Höhe als fundamentales Prinzip
- Unendliche Rotationssymmetrie: Symmetrie um jede Achse durch die Zylinderachse
- Parallele Grundflächen: Identische Kreise in konstantem Abstand h
- Geradlinige Mantellinien: Alle Mantellinien parallel zur Zylinderachse
Universelle Anwendungen
Behälterbau-Perfektion
Druckbehälter und Lagertanks nutzen die rotationssymmetrische Form für optimale Druckverteilung und maximale Materialeffizienz bei minimalem Oberflächeninhalt.
Maschinenbau-Präzision
Motorzylinder und Hydraulikzylinder verwenden die zylindrische Form für präzise Kolbenbewegungen und optimale Abdichtung bei minimaler Reibung.
Architektonische Eleganz
Säulen und Stützen nutzen die zylindrische Form für strukturelle Stabilität und ästhetische Wirkung mit klassischer zeitloser Schönheit.
Wissenschaftliche Präzision
Messzylinder und Laborgeräte verwenden die zylindrische Form für exakte Volumenbestimmung und reproduzierbare Messungen in der Forschung.
Zusammenfassung
Der Kreiszylinder verkörpert die perfekte Synthese aus geometrischer Einfachheit und praktischer Funktionalität. Seine durch die fundamentalen Formeln V = πr²h und S = 2πr² + 2πrh beschriebene Form zeigt die mathematische Schönheit rotationssymmetrischer Körper. Die Mantelfläche L = 2πrh als Abwicklung zu einem Rechteck demonstriert, wie dreidimensionale Komplexität in zweidimensionale Einfachheit überführt werden kann. Von präzisen Messzylindern über robuste Druckbehälter bis hin zu eleganten architektonischen Säulen - der Kreiszylinder beweist, dass die einfachsten geometrischen Formen oft zu den vielseitigsten und funktionalsten Lösungen führen. Er ist der lebende Beweis dafür, dass geometrische Perfektion nicht nur mathematische Eleganz besitzt, sondern auch praktische Anwendungen von höchster Effizienz ermöglicht und zeigt, wie Rotationssymmetrie und Kreisgeometrie in perfekter Harmonie die Grundlage für unzählige technische Innovationen schaffen.
|
|
|
|