Zylinder-Sektor Rechner
Rechner und Formeln zur Berechnung eines Zylinder-Sektors
Zylinder-Sektor Rechner
Der Zylinder-Sektor
Der Zylinder-Sektor ist ein sektorförmiger Zylinderabschnitt mit definiertem Zentralwinkel φ.
Zylinder-Sektor Eigenschaften
Der Zylinder-Sektor: Sektorförmiger Ausschnitt aus einem Kreiszylinder
Zylinder-Sektor Visualisierung
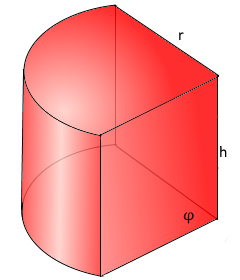
Zylinder-Sektor
Sektorförmiger Zylinderabschnitt
Parameter
r: Radius des Zylinders
h: Höhe des Zylinder-Sektors
φ: Zentralwinkel (in Grad)
AB: Sektorförmige Basisfläche
Sektorförmiger Zylinderabschnitt.
Definiert durch Zentralwinkel φ.
|
|
Was ist ein Zylinder-Sektor?
Der Zylinder-Sektor ist ein wichtiger geometrischer Körper:
- Definition: Sektorförmiger Ausschnitt aus einem Kreiszylinder
- Zentralwinkel φ: Bestimmt die Größe des Sektorausschnitts
- Eigenschaften: Kreissektor als Grundfläche und Deckfläche
- Seitenflächen: Rechteckige Schnittflächen an den Seiten
- Anwendung: Maschinenbau, Architektur, Rohrleitungstechnik
- Mathematik: Kombination aus Sektor- und Zylindergeometrie
Geometrische Eigenschaften des Zylinder-Sektors
Der Zylinder-Sektor zeigt charakteristische geometrische Eigenschaften:
Grundparameter
- Radius r: Radius der kreisförmigen Grundfläche
- Höhe h: Höhe des Zylinder-Sektors
- Zentralwinkel φ: Winkel des Sektorausschnitts (in Grad)
- Basisfläche AB: Sektorförmige Grund- und Deckfläche
Besondere Eigenschaften
- Sektorförmiger Querschnitt: Kreissektor als charakteristische Grundfläche
- Rechteckige Seitenflächen: Ebene Schnittflächen an den Radien
- Gekrümmte Mantelfläche: Zylindrischer Mantelabschnitt
- Winkelabhängige Größen: Alle Flächen proportional zu φ/360°
Mathematische Beziehungen des Zylinder-Sektors
Der Zylinder-Sektor folgt eleganten mathematischen Gesetzen:
Volumen-Formel
Volumen proportional zum Zentralwinkel. Elegante Sektorbeziehung.
Basisflächen-Formel
Sektorförmige Basisfläche als Bruchteil der Vollkreisfläche.
Anwendungen des Zylinder-Sektors
Zylinder-Sektoren finden Anwendung in verschiedenen Bereichen:
Maschinenbau & Automotive
- Getriebe-Segmente
- Kupplungs-Sektoren
- Turbinenrad-Abschnitte
- Ventilgehäuse-Teile
Architektur & Bauwesen
- Säulen-Segmente
- Gewölbe-Abschnitte
- Treppengeländer-Elemente
- Dach-Konstruktionen
Rohrleitungstechnik
- Rohrbogen-Sektoren
- Abzweig-Elemente
- Ventil-Segmente
- Flansch-Komponenten
Verfahrenstechnik
- Reaktor-Sektoren
- Behälter-Segmente
- Mischeinrichtungen
- Wärmetauscher-Teile
Formeln zum Zylinder-Sektor
Volumen (V)
Volumen proportional zum Zentralwinkel
Basisfläche (AB)
Sektorförmige Grund- und Deckfläche
Seitenfläche (AS)
Rechteckige Schnittfläche an den Radien
Mantelfläche (L)
Gekrümmte Zylinderoberfläche
Gesamtoberfläche (S)
Summe aller Teilflächen: zwei Basisflächen, zwei Seitenflächen und Mantelfläche
Weitere Parameter
\[b = \frac{2\pi r \phi}{360°}\]
\[\phi_{rad} = \frac{\phi \cdot \pi}{180°}\]
\[\frac{\phi}{360°} = \text{Anteil}\]
\[\text{Radius } r\]
Der Zylinder-Sektor verbindet 2D-Sektorgeometrie mit 3D-Zylinderform
Berechnungsbeispiel für einen Zylinder-Sektor
Gegeben
Gesucht: Alle Parameter des Zylinder-Sektors
1. Basisfläche berechnen
Für r = 5 cm, φ = 90°:
\[A_B = \frac{r^2 \pi \phi}{360°}\] \[A_B = \frac{5^2 \cdot \pi \cdot 90°}{360°}\] \[A_B = \frac{25\pi \cdot 90°}{360°} = \frac{25\pi}{4}\] \[A_B ≈ 19.63 \text{ cm}^2\]Die Basisfläche beträgt etwa 19.63 cm²
2. Seitenfläche berechnen
Rechteckige Schnittflächen:
\[A_S = r \cdot h\] \[A_S = 5 \cdot 6 = 30 \text{ cm}^2\]Zwei Seitenflächen:
\[2 \cdot A_S = 2 \cdot 30 = 60 \text{ cm}^2\]Die Seitenflächen betragen zusammen 60 cm²
3. Mantelfläche berechnen
Gekrümmte Zylinderoberfläche:
\[L = \frac{2\pi r h \phi}{360°}\] \[L = \frac{2\pi \cdot 5 \cdot 6 \cdot 90°}{360°}\] \[L = \frac{60\pi \cdot 90°}{360°} = 15\pi\] \[L ≈ 47.12 \text{ cm}^2\]Die Mantelfläche beträgt etwa 47.12 cm²
4. Volumen berechnen
Volumen des Zylinder-Sektors:
\[V = \frac{\pi r^2 h \phi}{360°}\] \[V = \frac{\pi \cdot 25 \cdot 6 \cdot 90°}{360°}\] \[V = \frac{150\pi \cdot 90°}{360°} = \frac{150\pi}{4}\] \[V ≈ 117.81 \text{ cm}^3\]Das Volumen beträgt etwa 117.81 cm³
5. Gesamtoberfläche berechnen
Summe aller Teilflächen:
\[S = 2A_B + 2A_S + L\] \[S = 2 \cdot 19.63 + 60 + 47.12\] \[S = 39.26 + 60 + 47.12 = 146.38 \text{ cm}^2\]Die Gesamtoberfläche beträgt etwa 146.38 cm²
6. Geometrische Analyse
90°/360° = 1/4 = 25% des Vollzylinders
V_voll = πr²h = π·25·6 ≈ 471.24 cm³
117.81/471.24 = 25.0% (exakt!)
Der Sektor entspricht exakt 25% des Vollzylinders - perfekte Sektorgeometrie!
7. Zusammenfassung
Der Zylinder-Sektor mit 90° - ein perfektes Viertel des Vollzylinders
8. Praktisches Beispiel: Getriebe-Segment
V ≈ 117.81 cm³
≈ 0.12 Liter
S ≈ 146.38 cm²
Beschichtungsfläche
90° Sektor
Viertel-Symmetrie
Ein Getriebe-Segment mit 90° Sektor für optimale Kraftübertragung
9. Weitere Winkel-Beispiele
V ≈ 58.90 cm³
12.5% des Vollzylinders
V ≈ 157.08 cm³
33.3% des Vollzylinders
V ≈ 235.62 cm³
Halbzylinder
Verschiedene Sektorgrößen für unterschiedliche Anwendungen
Der Zylinder-Sektor: Eleganz der 3D-Sektorgeometrie
Der Zylinder-Sektor ist ein faszinierender geometrischer Körper, der die Eleganz der zweidimensionalen Sektorgeometrie mit der Praktikabilität dreidimensionaler Zylinderformen verbindet. Als sektorförmiger Ausschnitt aus einem Kreiszylinder vereint er in sich die mathematische Klarheit proportionaler Winkelbeziehungen mit der technischen Anwendbarkeit in Maschinenbau, Architektur und Verfahrenstechnik. Diese einzigartige Kombination aus sektorialer Präzision und zylindrischer Funktionalität macht ihn zu einem unverzichtbaren Element in der modernen Konstruktionstechnik.
Die Geometrie der Sektorform
Der Zylinder-Sektor zeigt die Perfektion dreidimensionaler Sektorgeometrie:
- Zentralwinkel φ: Bestimmt alle Größenverhältnisse proportional zu φ/360°
- Sektorförmige Basisflächen: AB = (πr²φ)/360° als charakteristische Grundfläche
- Rechteckige Seitenflächen: AS = r·h als ebene Schnittflächen an den Radien
- Gekrümmte Mantelfläche: L = (2πrhφ)/360° als Zylinderabschnitt
- Volumenproportionalität: V = (πr²hφ)/360° direkt proportional zum Winkel
- Oberflächensymmetrie: S = 2AB + 2AS + L mit allen Komponenten
- Winkel-Invarianz: Alle Größen skalieren linear mit φ
Vielseitige Anwendungen
Maschinenbau-Präzision
Getriebe-Segmente und Kupplungs-Sektoren nutzen die präzise Winkelgeometrie für optimale Kraftübertragung und gleichmäßige Lastverteilung in rotierenden Systemen.
Architektonische Innovation
Säulen-Segmente und Gewölbe-Abschnitte verwenden die Sektorform für strukturell stabile und ästhetisch ansprechende Bauwerke mit charakteristischer radialer Symmetrie.
Rohrleitungs-Effizienz
Rohrbogen-Sektoren und Abzweig-Elemente nutzen die Sektorgeometrie für strömungsoptimierte Verbindungen mit minimalen Druckverlusten und gleichmäßiger Durchflussverteilung.
Verfahrenstechnische Perfektion
Reaktor-Sektoren und Behälter-Segmente verwenden die proportionalen Größenverhältnisse für präzise Prozesssteuerung und optimierte Wärme- und Stoffübertragung.
Zusammenfassung
Der Zylinder-Sektor verkörpert die perfekte Synthese aus geometrischer Proportionalität und praktischer Funktionalität. Seine durch den Zentralwinkel φ charakterisierte Form, beschrieben durch die eleganten proportionalen Formeln V = (πr²hφ)/360° und AB = (πr²φ)/360°, zeigt die mathematische Schönheit linearer Skalierung. Die Gesamtoberfläche S = 2AB + 2AS + L als Summe aller Teilflächen demonstriert, wie komplexe dreidimensionale Formen systematisch aufgebaut werden. Von präzisen Getriebe-Segmenten über elegante Säulen-Abschnitte bis hin zu strömungsoptimierten Rohrbogen-Sektoren - der Zylinder-Sektor beweist, dass die einfachsten mathematischen Beziehungen oft zu den funktionalsten technischen Lösungen führen. Er ist der lebende Beweis dafür, dass Sektorgeometrie nicht nur zweidimensionale Eleganz besitzt, sondern auch dreidimensionale Anwendungen von höchster Präzision ermöglicht und zeigt, wie Winkelproportionalität und Zylinderform in perfekter mathematischer Harmonie verschmelzen.
|
|
|
|