Verdreht Verlängerte Quadratbipyramide Rechner
Rechner und Formeln zur verdrehten, verlängerte Quadratbipyramide (Johnson Körper J17)
Verlängerte Pyramide Rechner
Die Verdreht Verlängerte Quadratbipyramide
Die verdreht verlängerte Quadratbipyramide ist ein Johnson Körper (J17) bestehend aus 16 gleichseitigen Dreiecken.
Johnson Körper J17 Eigenschaften
Die verdrehte Pyramide: Komplex konstruiert aus 16 Dreiecken
Verdrehte Pyramide Struktur
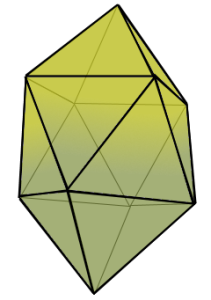
Die verdrehte Quadratpyramide mit komplexer Struktur.
Johnson Körper J17.
|
|
Was ist eine verdreht verlängerte Quadratbipyramide?
Die verdreht verlängerte Quadratbipyramide ist ein komplexer Johnson Körper:
- Definition: Verdrehte Verlängerung einer Quadratbipyramide
- Johnson Körper: J17 in der Klassifikation
- Flächen: 16 kongruente gleichseitige Dreiecke
- Ecken: 10 Ecken insgesamt
- Kanten: 24 Kanten verschiedener Typen
- Symmetrie: Komplexe D4d-Symmetrie
Geometrische Eigenschaften der verdrehten Pyramide
Die verdreht verlängerte Quadratbipyramide zeigt komplexe geometrische Eigenschaften:
Grundparameter
- Flächen: 16 gleichseitige Dreiecke
- Ecken: 10 Ecken verschiedener Typen
- Kanten: 24 Kanten (alle gleich lang)
- Euler-Charakteristik: V - E + F = 10 - 24 + 16 = 2
Besondere Eigenschaften
- Deltaeder: Alle Flächen sind Dreiecke
- Gleichseitig: Alle Dreiecke sind gleichseitig
- Verdreht: Gyroelongation durch Verdrehung
- Konvex: Keine einspringenden Kanten oder Ecken
Mathematische Beziehungen
Die verdreht verlängerte Quadratbipyramide folgt komplexen mathematischen Gesetzen:
Volumen-Formel
Enthält komplexe Quadratwurzeln. Verdrehte Eleganz.
Oberflächen-Formel
16 gleichseitige Dreiecke. Einfache √3 Beziehung.
Anwendungen der verdrehten Pyramide
Verdreht verlängerte Quadratbipyramiden finden Anwendung in verschiedenen Bereichen:
Architektur & Bauwesen
- Komplexe Dachstrukturen
- Moderne Pavillon-Designs
- Strukturelle Knotenelemente
- Geometrische Fassadenelemente
Wissenschaft & Technik
- Komplexe Kristallstrukturen
- Molekulare Komplexe
- Optische Bauteile
- Präzisionsmechanik
Bildung & Lehre
- Erweiterte Geometrie-Studien
- Johnson Körper Forschung
- Komplexe 3D-Geometrie
- Symmetrie-Untersuchungen
Kunst & Design
- Komplexe Skulpturen
- Geometrische Installationen
- Designer-Objekte
- Kunsthandwerk
Formeln zur verdrehten verlängerten Quadratbipyramide
Volumen (V)
Volumen mit komplexen Quadratwurzeln für verdrehte Geometrie
Höhe (h)
Höhe mit komplexer Beziehung für verdrehte Struktur
Oberfläche (S)
16 gleichseitige Dreiecke mit √3 Beziehung
Johnson Körper
17. Johnson Körper in der Klassifikation
Verdrehte Pyramide Parameter
16 gleichseitige △
10 Ecken
24 Kanten
D4d
Alle Eigenschaften folgen aus der verdrehten Verlängerung der Quadratbipyramide
Berechnungsbeispiel für eine verdreht verlängerte Quadratbipyramide
Gegeben
Gesucht: Alle Eigenschaften der verdreht verlängerten Quadratbipyramide
1. Volumen-Berechnung
Für a = 10:
\[V = \frac{(\sqrt{2} + \sqrt{ 4 + 3 \cdot \sqrt{2}})}{3} \cdot 10^3\] \[V ≈ 1.4284 \cdot 1000\] \[V ≈ 1428.4\]Das Volumen beträgt etwa 1428.4 Volumeneinheiten
2. Oberflächen-Berechnung
Für a = 10:
\[S = 4 \cdot \sqrt{3} \cdot 10^2\] \[S ≈ 6.9282 \cdot 100\] \[S ≈ 692.82\]Die Oberfläche beträgt etwa 692.82 Flächeneinheiten
3. Höhen-Berechnung
Für a = 10:
\[h = \left( \sqrt{1 - \frac{1}{(2+\sqrt{2})}} + \frac{2}{\sqrt{2}} \right) \cdot 10\] \[h ≈ 2.255 \cdot 10\] \[h ≈ 22.55\]Die Höhe beträgt etwa 22.55 Längeneinheiten
4. Die perfekte verdrehte Pyramide
Die verdreht verlängerte Quadratbipyramide mit komplexer Symmetrie
Die verdreht verlängerte Quadratbipyramide: Komplexe Geometrie in perfekter Form
Die verdreht verlängerte Quadratbipyramide ist ein faszinierender Johnson Körper, der die Komplexität der dreidimensionalen Geometrie in ihrer ganzen Pracht zeigt. Durch die Verdrehung (Gyroelongation) einer gewöhnlichen Quadratbipyramide entsteht eine einzigartige Struktur mit 16 kongruenten gleichseitigen Dreiecken, die diesen Körper zu einem der anspruchsvollsten Beispiele für geometrische Komplexität macht. Die mathematische Schönheit liegt in den verschachtelten Quadratwurzeln und komplexen Beziehungen, die alle geometrischen Eigenschaften elegant miteinander verknüpfen.
Die Geometrie der verdrehten Komplexität
Die verdreht verlängerte Quadratbipyramide zeigt die Perfektion der komplexen Symmetrie:
- Deltaeder: Alle 16 Flächen sind kongruente gleichseitige Dreiecke
- D4d-Symmetrie: Vierzählige Rotationssymmetrie mit Verdrehung
- Uniformität: Alle 24 Kanten haben dieselbe Länge
- Johnson Körper: J17 in der klassischen Klassifikation
- Konvexität: Alle Ecken ragen nach außen
- Gyroelongation: Verdrehte Verlängerung als konstruktives Prinzip
- Komplexität: Ideal für anspruchsvolle geometrische Studien
Mathematische Eleganz in der Komplexität
Verschachtelte Quadratwurzeln
Die Formeln der verdreht verlängerten Quadratbipyramide zeigen mathematische Komplexität mit verschachtelten Quadratwurzeln wie √(4 + 3√2), die die verdrehte Geometrie beschreiben.
Gyroelongation-Prinzip
Die Verdrehung (Gyroelongation) erzeugt komplexe Beziehungen zwischen den geometrischen Parametern und führt zu faszinierenden mathematischen Strukturen.
Strukturelle Komplexität
Die 16 Dreiecke bilden eine komplexe Struktur mit verschiedenen Ecktypen und vielfältigen geometrischen Beziehungen.
Ästhetische Vollendung
Die verdrehte Verlängerung erzeugt eine einzigartige visuelle Dynamik zwischen Ordnung und Komplexität, Symmetrie und Bewegung.
Zusammenfassung
Die verdreht verlängerte Quadratbipyramide verkörpert die faszinierende Komplexität der dreidimensionalen Geometrie in ihrer anspruchsvollsten Form. Ihre Struktur aus sechzehn gleichseitigen Dreiecken, beschrieben durch verschachtelte Quadratwurzel-Formeln mit eleganten mathematischen Beziehungen, macht sie zu einem herausfordernden Studienobjekt für Mathematiker, Architekten und Designer. Als Johnson Körper J17 zeigt sie, wie die Verdrehung (Gyroelongation) einfacher geometrischer Formen zu völlig neuen Welten der Komplexität führen kann. Von der reinen Mathematik bis zur praktischen Anwendung bleibt die verdreht verlängerte Quadratbipyramide ein faszinierendes Beispiel für die Kraft der geometrischen Transformation und die Schönheit der komplexen Symmetrie in perfekter Form.
|
|
|
|