Fünfeckpyramide Rechner
Rechner und Formeln zur Fünfeckpyramide (Johnson Körper J2)
Fünfeckpyramide Rechner
Die Fünfeckpyramide
Die Fünfeckpyramide ist ein Johnson Körper (J2) mit regelmäßiger Fünfeck-Basis und goldenem Schnitt φ!
Johnson Körper J2 Eigenschaften
Die Pentagon-Pyramide: Regelmäßige Fünfeck-Basis mit Dreiecks-Seiten
Fünfeckpyramide Struktur
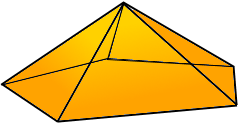
Die Fünfeckpyramide mit regelmäßiger Pentagon-Basis.
Johnson Körper J2 mit goldenem Schnitt φ.
|
|
Was ist eine Fünfeckpyramide?
Die Fünfeckpyramide ist ein eleganter Johnson Körper mit goldenem Schnitt:
- Definition: Pyramide mit regelmäßiger Fünfeck-Basis
- Johnson Körper: J2 in der Klassifikation
- Flächen: 1 regelmäßiges Fünfeck + 5 gleichseitige Dreiecke
- Ecken: 6 Ecken (5 an der Basis + 1 Spitze)
- Kanten: 10 Kanten (alle gleich lang)
- Symmetrie: C5v-Symmetrie mit φ
Geometrische Eigenschaften der Fünfeckpyramide
Die Fünfeckpyramide zeigt bemerkenswerte geometrische Eigenschaften mit goldenem Schnitt φ = (1+√5)/2:
Grundparameter
- Flächen: 6 Flächen (1 Fünfeck + 5 Dreiecke)
- Ecken: 6 Ecken (5 an der Basis, 1 an der Spitze)
- Kanten: 10 Kanten (alle gleich lang)
- Euler-Charakteristik: V - E + F = 6 - 10 + 6 = 2 ✓
Besondere Eigenschaften
- Goldener Schnitt: φ = (1+√5)/2 ≈ 1.618
- Pentagonale Symmetrie: Fünfzählige Rotationsachse
- Reguläres Fünfeck: Basis ist regelmäßiges Pentagon
- Konvex: Keine einspringenden Kanten oder Ecken
Mathematische Beziehungen mit goldenem Schnitt
Die Fünfeckpyramide folgt den eleganten Gesetzen des goldenen Schnitts φ:
Volumen-Formel
Pyramidenvolumen mit Fünfeck-Basis. Elegant mit goldenem Schnitt φ.
Oberflächen-Formel
Kombination aus Fünfeck und gleichseitigen Dreiecken. Komplexe √5 und φ Beziehungen.
Anwendungen der Fünfeckpyramide
Fünfeckpyramiden finden Anwendung in verschiedenen Bereichen:
Architektur & Bauwesen
- Pentagon-basierte Pyramiden
- Dachkonstruktionen mit goldenem Schnitt
- Moderne Strukturen und Pavillons
- Dekorative Spitzen und Türme
Wissenschaft & Technik
- Kristallographische Strukturen
- Molekulare Modelle mit φ-Symmetrie
- Pentagonale Materialstrukturen
- Geodätische Konstruktionen
Bildung & Lehre
- Goldener Schnitt Demonstration
- Pentagonale Geometrie-Studien
- Johnson Körper Klassifikation
- Pyramiden-Geometrie
Kunst & Design
- Goldener Schnitt Skulpturen
- Pentagon-basierte Kunstwerke
- Harmonische Proportionen
- Schmuckdesign mit φ
Formeln zur Fünfeckpyramide
Volumen (V)
Pyramidenvolumen mit goldenem Schnitt φ Beziehungen
Oberfläche (S)
1 regelmäßiges Fünfeck + 5 gleichseitige Dreiecke
Höhe (h)
Höhe mit √5 für optimale Pentagon-Proportionen
Johnson Körper
2. Johnson Körper in der Klassifikation
Fünfeckpyramide Parameter mit goldenem Schnitt φ
1⬟ + 5△
6 Ecken
10 Kanten
C5v
φ = (1+√5)/2
Alle Eigenschaften folgen aus der pentagonalen Symmetrie mit φ
Berechnungsbeispiel für eine Fünfeckpyramide
Gegeben
Gesucht: Alle Eigenschaften der Fünfeckpyramide mit goldenem Schnitt
1. Volumen-Berechnung
Für a = 10:
\[V = \frac{5+\sqrt{5}}{24} \cdot 10^3\] \[V ≈ 0.3015 \cdot 1000\] \[V ≈ 301.5\]Das Volumen beträgt etwa 301.5 Volumeneinheiten
2. Oberflächen-Berechnung
Für a = 10:
\[S = \frac{100}{2}\sqrt{\frac{5}{2}(10+\sqrt{5}+\sqrt{75+30\sqrt{5}})}\] \[S ≈ 3.8855 \cdot 100\] \[S ≈ 388.55\]Die Oberfläche beträgt etwa 388.55 Flächeneinheiten
3. Höhen-Berechnung
Für a = 10:
\[h = \sqrt{\frac{5-\sqrt{5}}{10}} \cdot 10\] \[h ≈ 0.5257 \cdot 10\] \[h ≈ 5.257\]Die Höhe beträgt etwa 5.257 Längeneinheiten
4. Die perfekte Fünfeckpyramide mit goldenem Schnitt
Die Fünfeckpyramide mit goldenem Schnitt φ und pentagonaler Eleganz
Die Fünfeckpyramide: Pentagonale Eleganz mit goldenem Schnitt
Die Fünfeckpyramide ist ein eleganter Johnson Körper, der die zeitlose Schönheit des goldenen Schnitts φ = (1+√5)/2 ≈ 1.618 in einer klassischen Pyramidenform verkörpert. Mit ihrer regelmäßigen Pentagon-Basis und den fünf gleichseitigen Dreiecken als Seitenflächen vereint sie mathematische Perfektion mit architektonischer Eleganz. Die mathematische Schönheit liegt in den eleganten Beziehungen mit √5 und dem goldenen Schnitt φ, die alle geometrischen Eigenschaften harmonisch miteinander verknüpfen und diese Struktur zu einem der faszinierendsten Beispiele für pentagonale Geometrie machen.
Die Geometrie der pentagonalen Perfektion
Die Fünfeckpyramide zeigt die Eleganz der pentagonalen Symmetrie mit φ:
- Pentagonale Basis: Regelmäßiges Fünfeck mit goldenem Schnitt φ
- C5v-Symmetrie: Fünfzählige Rotationssymmetrie mit vertikalen Spiegelebenen
- Uniformität: Alle 10 Kanten haben dieselbe Länge
- Johnson Körper: J2 - einer der ersten in der Klassifikation
- Konvexität: Alle Ecken ragen nach außen
- Goldener Schnitt: φ-Verhältnisse in den Pentagon-Proportionen
- Pyramidale Eleganz: Klassische Pyramidenform mit pentagonaler Basis
Mathematische Eleganz mit φ
Goldener Schnitt Harmonie
Die Formeln der Fünfeckpyramide zeigen die tiefe Verbindung zum goldenen Schnitt φ mit √5-Beziehungen, die die natürlichen Proportionen der pentagonalen Harmonie beschreiben.
Klassische Pyramidenform
Die Kombination von Pentagon-Basis und dreieckigen Seitenflächen schafft eine perfekte Balance zwischen Stabilität und der zeitlosen Schönheit des φ-Verhältnisses.
Pentagonale Perfektion
Die Fünfeckpyramide zeigt, wie der goldene Schnitt von der zweidimensionalen Pentagon-Geometrie in dreidimensionale Formen überführt werden kann.
Ästhetische Vollendung
Die harmonische Verbindung von regelmäßigem Fünfeck und gleichseitigen Dreiecken erzeugt eine einzigartige visuelle Dynamik des goldenen Schnitts in Pyramidenform.
Zusammenfassung
Die Fünfeckpyramide verkörpert die perfekte Synthese zwischen dem goldenen Schnitt φ und der klassischen Pyramidenform. Ihre Struktur aus einem regelmäßigen Fünfeck und fünf gleichseitigen Dreiecken, beschrieben durch elegante φ- und √5-Formeln, macht sie zu einem faszinierenden Studienobjekt für Mathematiker, Architekten und alle, die sich für die Schönheit der pentagonalen Harmonie begeistern. Als Johnson Körper J2 zeigt sie, wie der goldene Schnitt in einfachster und elegantester Form in die dreidimensionale Geometrie überführt werden kann. Von der reinen Mathematik bis zur praktischen Anwendung bleibt die Fünfeckpyramide ein herausragendes Beispiel für die Kraft des goldenen Schnitts und die zeitlose Schönheit der pentagonalen Geometrie.
|
|
|
|