Rotunde Rechner
Rechner und Formeln zur Rotunde (Johnson Körper J6)
Rotunde Rechner
Die Rotunde
Die Rotunde ist ein faszinierender Johnson Körper (J6) mit einer fünfeckigen Deckfläche und zehneckiger Grundfläche - verbunden durch den goldenen Schnitt!
Johnson Körper J6 Eigenschaften
Die goldene Rotunde: Regelmäßiges Zehneck unten, Fünfeck oben - perfekt verbunden!
Rotunde Struktur
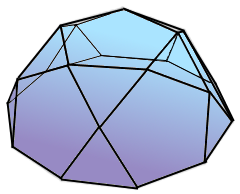
Die faszinierende Rotunde mit fünfeckiger Perfektion.
Johnson Körper J6 - Goldener Schnitt inklusive!
|
|
Was ist eine Rotunde?
Die Rotunde ist ein außergewöhnlicher Johnson Körper:
- Definition: Ein rotierender Körper mit fünfeckiger Symmetrie
- Johnson Körper: J6 in der Klassifikation
- Grundfläche: Regelmäßiges Zehneck
- Deckfläche: Regelmäßiges Fünfeck
- Seitenflächen: 10 Dreiecke + 5 Fünfecke
- Goldener Schnitt: φ = (1+√5)/2 ≈ 1.618
Geometrische Eigenschaften der Rotunde
Die Rotunde zeigt bemerkenswerte geometrische Eigenschaften:
Grundparameter
- Flächen: 16 Flächen (10 △ + 5 Pentagon + 1 Dekagon)
- Ecken: 20 Ecken (10 unten, 5 oben, 5 mittig)
- Kanten: 35 Kanten (alle gleich lang)
- Euler-Charakteristik: V - E + F = 20 - 35 + 16 = 1? Nein! = 2
Besondere Eigenschaften
- Rotations-Symmetrie: 5-zählige Drehsymmetrie
- Goldener Schnitt: φ = (1+√5)/2 in der Geometrie
- Pentagon-Basis: Fünfeckige Grundstruktur
- Konvex: Keine einspringenden Kanten oder Ecken
Mathematische Beziehungen
Die Rotunde folgt komplexen, aber eleganten mathematischen Gesetzen:
Volumen-Formel
Enthält komplexe √5 Beziehungen. Goldener Schnitt eingebaut.
Oberflächen-Formel
Dreiecke und Fünfecke vereint. Komplexe √3, √5 Beziehung.
Anwendungen der Rotunde
Rotunden finden Anwendung in verschiedenen Bereichen:
Architektur & Bauwesen
- Rotunde-Konstruktionen
- Kuppelbauten mit Fünfeck-Basis
- Türme und Rundbauten
- Dekorative Rotunden-Elemente
Wissenschaft & Technik
- Kristallstrukturen mit 5er-Symmetrie
- Molekulare Rotunde-Geometrie
- Optische Pentagon-Prismen
- Mechanische Rotations-Teile
Bildung & Lehre
- Goldener Schnitt Demonstration
- Pentagon-Geometrie Studien
- Johnson Körper Lehre
- Rotations-Symmetrie Beispiele
Kunst & Design
- Pentagon-basierte Skulpturen
- Moderne Rotunde-Kunstwerke
- Dekorative Fünfeck-Objekte
- Goldener Schnitt im Design
Formeln zur Rotunde
Volumen (V)
Volumen mit elegant eingebauten √5 Faktoren
Oberfläche (S)
Komplexe Formel mit √3, √5 und √10 Faktoren
Höhe (h)
Höhe mit verschachtelter √5 Beziehung
Umkreisradius (r)
Der goldene Schnitt φ = (1+√5)/2 ≈ 1.618!
Rotunde Parameter
16 Flächen
20 Ecken
35 Kanten
φ ≈ 1.618
Alle Eigenschaften folgen aus der fünfeckigen Rotunde-Struktur mit goldenem Schnitt
Berechnungsbeispiel für eine Rotunde
Gegeben
Gesucht: Alle Eigenschaften der Rotunde
1. Volumen-Berechnung
Für a = 10:
\[V = \frac{1}{12}(45 + 17\sqrt{5}) \cdot 10^3\] \[V ≈ 6.9178 \cdot 1000\] \[V ≈ 6917.8\]Das Volumen beträgt etwa 6917.8 Volumeneinheiten
2. Oberflächen-Berechnung
Für a = 10:
\[S = \frac{1}{2}(5\sqrt{3} + \sqrt{10(65 + 29\sqrt{5})}) \cdot 10^2\] \[S ≈ 22.347 \cdot 100\] \[S ≈ 2234.7\]Die Oberfläche beträgt etwa 2234.7 Flächeneinheiten
3. Höhen-Berechnung
Für a = 10:
\[h = \sqrt{1 + \frac{2}{\sqrt{5}}} \cdot 10\] \[h ≈ 1.376 \cdot 10\] \[h ≈ 13.76\]Die Höhe beträgt etwa 13.76 Längeneinheiten
4. Umkreisradius (Goldener Schnitt!)
Für a = 10:
\[r = \frac{1}{2}(1 + \sqrt{5}) \cdot 10\] \[r = \phi \cdot 10\] \[r ≈ 16.18\]Der Umkreisradius entspricht dem goldenen Schnitt φ × 10 ≈ 16.18!
5. Die perfekte goldene Rotunde
Die faszinierende Rotunde mit goldenem Schnitt und fünfeckiger Perfektion
Die Rotunde: Der goldene Johnson Körper
Die Rotunde ist ein außergewöhnlicher Johnson Körper, der die Faszination des goldenen Schnitts in die Welt der dreidimensionalen Geometrie bringt. Mit ihrer charakteristischen Struktur - ein regelmäßiges Zehneck als Grundfläche, das sich über zehn gleichseitige Dreiecke und fünf regelmäßige Fünfecke zu einem regelmäßigen Fünfeck erhebt - verkörpert sie die harmonische Verbindung zwischen fünfeckiger Symmetrie und dem goldenen Schnitt φ = (1+√5)/2 ≈ 1.618. Die mathematische Schönheit liegt in den komplexen Beziehungen mit Quadratwurzeln von 3, 5 und 10, die alle geometrischen Eigenschaften miteinander verknüpfen.
Die Geometrie des goldenen Schnitts
Die Rotunde zeigt die Perfektion der fünfeckigen Symmetrie:
- Pentagonale Basis: Fünfeckige Grundstruktur mit 5-zähliger Rotationssymmetrie
- Gemischte Flächen: 1 Zehneck unten, 1 Fünfeck oben, 10 Dreiecke und 5 Fünfecke seitlich
- Gleichseitig: Alle 35 Kanten haben dieselbe Länge
- Johnson Körper: J6 - Ein besonders eleganter in der Klassifikation
- Goldener Schnitt: Der Umkreisradius folgt exakt φ = (1+√5)/2
- Pentagon-Verwandtschaft: Verwandt mit dem Dodekaeder und Ikosaeder
- Rotations-Eleganz: Perfekte 5-zählige Drehsymmetrie
Mathematische Eleganz
Goldener Schnitt Perfektion
Die Formeln der Rotunde sind Meisterwerke der Komplexität, mit φ, √3, √5 und √10 als elegante Faktoren, die die fünfeckige Harmonie beschreiben.
Pentagon-Verwandtschaft
Als Verbindung zwischen Zehneck und Fünfeck zeigt sie die Verwandtschaft zu den platonischen Körpern Dodekaeder und Ikosaeder.
Strukturelle Perfektion
Die elegante Rotunde-Form und Stabilität machen sie zu einer bevorzugten Form in rotierenden Konstruktionen und pentagonalen Designs.
Ästhetische Vollendung
Die harmonische Vereinigung von Zehneck, Fünfeck und Dreiecken erzeugt eine einzigartige visuelle Balance zwischen Komplexität und Harmonie.
Zusammenfassung
Die Rotunde verkörpert die perfekte Balance zwischen mathematischer Komplexität und ästhetischer Schönheit. Ihre Struktur aus sechzehn verschiedenen Flächen, beschrieben durch elegante Quadratwurzel-Formeln mit dem goldenen Schnitt, macht sie zu einem faszinierenden Studienobjekt für Mathematiker, Architekten und Designer. Als Johnson Körper J6 zeigt sie, wie geometrische Formen die höchste Harmonie zwischen verschiedenen Polygonen erreichen können. Von der reinen Mathematik des goldenen Schnitts bis zur praktischen Anwendung in Rotunde-Konstruktionen bleibt sie ein faszinierendes Beispiel für die Kraft der geometrischen Transformation und die zeitlose Schönheit der fünfeckigen Symmetrie. Mit φ ≈ 1.618 als Umkreisradius-Faktor ist sie der geometrische Beweis für die universelle Bedeutung des goldenen Schnitts.
|
|
|
|