RMS value of a sawtooth voltage

Calculator and formulas for calculating the RMS value of a sawtooth voltage

Sawtooth Voltage Calculator

Symmetrical sawtooth voltage

This function calculates the RMS value of a symmetrical sawtooth voltage. The mean value is always 0 volts for a symmetrical voltage.

Peak voltage U_s

Decimal places

Result

RMS voltage:

Sawtooth voltage & parameters

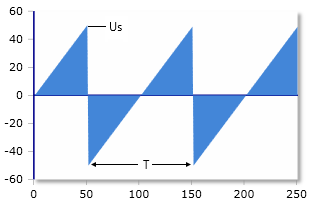
Parameters

\(\displaystyle U_s\) = Peak voltage [V]

\(\displaystyle U_{eff}\) = RMS voltage [V]

\(\displaystyle U_m\) = Mean voltage = 0V (symmetrical)

Basic formula

\[U_{eff} = \frac{U_s}{\sqrt{3}}\]

The RMS value is about 57.7% of the peak voltage.

Example calculations

Practical calculation examples

Example 1: Standard sawtooth voltage

Given: U_s = 100V

\[U_{eff} = \frac{100V}{\sqrt{3}} = \frac{100V}{1{,}732} = 57{,}7V\]

The RMS value is about 57.7% of the peak value

Example 2: Audio signal generator

Given: U_s = 10V (typical test signal)

\[U_{eff} = \frac{10V}{\sqrt{3}} = 5{,}77V\]

Used in sweep signal generation

Example 3: Oscilloscope time base

Given: U_s = 5V (time base signal)

\[U_{eff} = \frac{5V}{\sqrt{3}} = 2{,}89V\]

Application in ramp generators

Ratios for sawtooth voltage

RMS ratio:

U_eff / U_s: 1/√3 ≈ 0.577

Percent: ≈ 57.7%

Factor: 0.577

Mean value:

U_m: 0V (symmetrical)

Positive half-wave: Linearly rising

Negative half-wave: Linearly falling

Formula for sawtooth voltage

What is a sawtooth voltage?

The RMS value (root mean square) of a sawtooth voltage can be calculated as follows when the voltage is in periodic form. The RMS value is defined as the DC value with the same thermal effect as the considered AC value. For symmetrical sawtooth voltages, it is calculated as follows.

Definition of RMS value

In a symmetrical sawtooth voltage, the voltage rises linearly from -U_s to +U_s over half a period, and then falls linearly from +U_s to -U_s over the other half period. The mean value of the voltage is always 0 volts.

RMS value formula

\[U_{eff} = \frac{U_s}{\sqrt{3}}\]

The mean value of the voltage is always 0 volts for symmetrical sawtooth voltages.

Properties of the sawtooth wave

The sawtooth wave has a linear slope over the entire period. Unlike the triangle wave, there is no symmetrical rise and fall time - the voltage rises (or falls) continuously over the entire period. In a symmetrical sawtooth voltage, the signal swings between -U_s and +U_s, so the mean value is zero.

Mathematical derivation

For a symmetrical sawtooth wave with period T:

\[U_{eff} = \sqrt{\frac{1}{T} \int_0^T u^2(t) \, dt}\]

\[U_{eff} = \frac{U_s}{\sqrt{3}}\]

Comparison with other signals

Sine wave: U_eff = U_s/√2 ≈ 0.707

Triangle wave: U_eff = U_s/√3 ≈ 0.577

Sawtooth wave: U_eff = U_s/√3 ≈ 0.577

Square wave: U_eff = U_s = 1.0

Practical applications

Signal generation

Sweep generators
Frequency wobbling
VCO control
Ramp signals

Measurement technology

Oscilloscope time base
Spectrum analyzer
Linearity measurement
ADC test patterns

Synthesizer

Audio synthesizer
Sound shaping
Modulation sources
Effect generators

Spectral properties

Harmonic components

A sawtooth voltage contains all harmonics with a specific amplitude distribution:

\[u(t) = \frac{2U_s}{\pi} \sum_{n=1}^{\infty} \frac{(-1)^{n+1}}{n} \sin(n\omega t)\]

Fundamental: 2U_s/π ≈ 0.637 · U_s

2nd harmonic: U_s/π ≈ 0.318 · U_s

3rd harmonic: -2U_s/(3π) ≈ -0.212 · U_s

Special feature: Contains all harmonics (even and odd)

Design notes

Important properties

Linearity: Constant slope over the entire period
Symmetry: Mean value is zero for symmetrical sawtooth signals
Harmonics: Contains all harmonics with 1/n amplitude drop
Bandwidth: Sharp transitions require high bandwidth
Reset: Instant return to the start value at the end of the period
EMC: High harmonic content can cause interference

AC functions