Sine Pulse RMS Value (Half-Wave Rectification)

Calculator and formula for calculating the RMS and mean value of sine pulses

Sine Pulse Calculator (Half-Wave)

Half-Wave Rectification

This function calculates the RMS and mean value of a sine pulse from a half-wave rectification. Only the positive half-wave is used.

V
Results
RMS voltage:
Mean voltage:

Half-Wave Rectification

Sine pulse after half-wave rectification

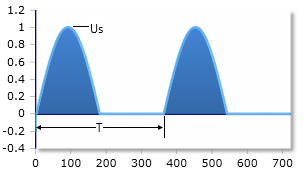
Sine pulse after half-wave rectification - only positive half-wave

Parameters
\(\displaystyle U_s\) = Peak voltage [V]
\(\displaystyle U_{eff}\) = RMS voltage [V]
\(\displaystyle U_m\) = Mean voltage [V]
Basic formulas
\[U_{eff} = \frac{U_s}{2}\]
\[U_m = \frac{U_s}{\pi}\]

Example calculations

Practical calculation examples

Example 1: Standard half-wave rectification

Given: Us = 10V (peak voltage of the sine wave)

\[U_{eff} = \frac{10V}{2} = 5{,}0V\]
\[U_m = \frac{10V}{\pi} = \frac{10V}{3{,}14159} = 3{,}18V\]
Typical half-wave rectification with 50% RMS value
Example 2: Rectified mains voltage

Given: Us = 325V (peak of 230V mains voltage)

\[U_{eff} = \frac{325V}{2} = 162{,}5V\]
\[U_m = \frac{325V}{\pi} = 103{,}5V\]
Half-wave rectification of mains voltage
Example 3: Low voltage application

Given: Us = 5V (small signal voltage)

\[U_{eff} = \frac{5V}{2} = 2{,}5V\]
\[U_m = \frac{5V}{\pi} = 1{,}59V\]
Typical for signal processing and sensors
Ratios for half-wave rectification
RMS ratio:
Ueff / Us: 1/2 = 0.5
Percent: 50%
Factor: 0.5
Mean value ratio:
Um / Us: 1/π ≈ 0.318
Percent: ≈ 31.8%
Factor: 0.318

Theory of Half-Wave Rectification

What is half-wave rectification?

To calculate the RMS voltage and the mean voltage (or average voltage) of a half-wave rectification, proceed step by step. In a half-wave rectification, only the positive part of the sinusoidal AC voltage is used. The negative half-wave is cut off or blocked.

RMS voltage after half-wave rectification

The RMS value is defined as the DC value with the same thermal effect as the considered AC value. For a sinusoidal AC voltage without rectification, the RMS value is Ueff = Us/√2.

After half-wave rectification, only the positive part of the sine wave is used, and the RMS voltage can be calculated with a different formula. It results from the quadratic mean over half a period:

RMS value formula
\[U_{eff} = \frac{U_s}{2}\]

The RMS value is exactly 50% of the peak voltage.

Mean voltage after half-wave rectification

Since we only use the positive part of the sine wave, the mean value of the voltage after half-wave rectification is:

Mean value formula
\[U_m = \frac{U_s}{\pi}\]

The mean value is about 31.8% of the peak voltage.

Mathematical derivation

Calculation of the RMS value

For a half-wave rectified sine over a full period T:

\[U_{eff} = \sqrt{\frac{1}{T} \int_0^T u^2(t) \, dt}\]
For 0 ≤ t ≤ T/2: u(t) = Us sin(ωt) (positive half-wave)
For T/2 < t ≤ T: u(t) = 0 (negative half-wave blocked)
\[U_{eff} = \sqrt{\frac{1}{T} \int_0^{T/2} U_s^2 \sin^2(\omega t) \, dt} = \frac{U_s}{2}\]
Calculation of the mean value

The mean value is calculated over a full period:

\[U_m = \frac{1}{T} \int_0^T u(t) \, dt\]
\[U_m = \frac{1}{T} \int_0^{T/2} U_s \sin(\omega t) \, dt = \frac{U_s}{\pi}\]

Practical applications

Power supplies
  • Simple rectifiers
  • Low cost
  • High ripple voltage
  • Low efficiency
Signal processing
  • Envelope detector
  • AM demodulation
  • Peak value measurement
  • Rectification of weak signals
Measurement technology
  • Simple RMS measurement
  • Average value measurement
  • Calibration circuits
  • Reference voltages

Comparison with other rectifications

Rectification comparison
No rectification:
Ueff = Us/√2 ≈ 0.707
Um = 0V
Half-wave rectification:
Ueff = Us/2 = 0.5
Um = Us/π ≈ 0.318
Full-wave rectification:
Ueff = Us/√2 ≈ 0.707
Um = 2Us/π ≈ 0.637

Design notes

Practical considerations
  • Low efficiency: Only 50% of the available energy is used
  • High ripple voltage: 100% ripple at mains frequency
  • Transformer utilization: Poor utilization of the iron core
  • Diode load: High peak current in short pulses
  • Filtering effort: Large capacitors required for smoothing
  • Application: Only for non-critical applications or very low power


AC functions

Alternating voltage values  •  Alternating voltage and time  •  Frequency and wavelength  •  Alternating voltage value and angle  •  Frequency and periodic time  •  RMS value of a sinusoidal oscillation  •  RMS value of a sinusoidal oscillation with offset  •  RMS value of a sine pulse (half-wave rectification)  •  RMS value of a sine pulse (full-wave rectification)  •  RMS value of a square wave voltage  •  RMS value of a square pulse  •  RMS value of a triangle voltage  •  RMS value of a triangular pulse  •  RMS value of a sawtooth voltage  •  RMS value of a sawtooth pulse  •