Frequency and Period

Calculator and formulas for calculating frequency and period of AC voltages

Period and Frequency Calculator

Frequency-Period Calculator

On this page you can calculate the duration of the period for a certain frequency, or the frequency for a given period. Essential for AC voltage analysis and oscillation calculations.

What should be calculated?

Calculate period T

Calculate frequency f

Frequency f

Period T

Decimal places

Result

Period:

Frequency:

Frequency & Period

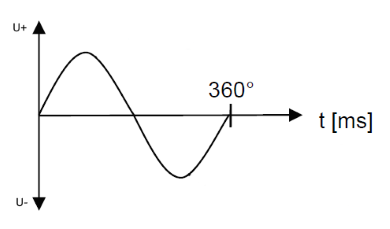
Period T of a periodic oscillation

Parameters

\(\displaystyle f\) = Frequency [Hz]

\(\displaystyle T\) = Period duration [s]

\(\displaystyle \omega\) = Angular frequency [rad/s]

Basic formulas

\[f = \frac{1}{T}\]

\[T = \frac{1}{f}\]

Tip

A calculator for calculating frequency and wavelengths can be found here.

Example calculations

Practical calculation examples

Example 1: Mains frequency (50Hz)

Given: f = 50Hz (European mains frequency)

\[T = \frac{1}{f} = \frac{1}{50Hz} = 0.02s = 20ms\]

One period of mains voltage lasts 20 milliseconds

Example 2: Audio frequency (1kHz)

Given: f = 1kHz (typical test tone)

\[T = \frac{1}{1000Hz} = 0.001s = 1ms\]

High audio frequency with 1ms period

Example 3: Radio frequency (100MHz)

Given: f = 100MHz (FM radio)

\[T = \frac{1}{100 \times 10^6Hz} = 10 \times 10^{-9}s = 10ns\]

Very short period in the nanosecond range

Frequency ranges

Audio frequencies:

20Hz: T = 50ms

1kHz: T = 1ms

20kHz: T = 50µs

Radio frequencies:

1MHz: T = 1µs

100MHz: T = 10ns

1GHz: T = 1ns

Mains frequencies:

50Hz: T = 20ms

60Hz: T = 16.67ms

400Hz: T = 2.5ms

Clock frequencies:

1MHz: T = 1µs

100MHz: T = 10ns

3GHz: T = 0.33ns

Formulas for Frequency and Period

Basic relationships

The frequency is the number of periods per second. It indicates how often a periodic process repeats in one second. The unit of frequency is Hertz (Hz).

The period is the duration of one complete oscillation cycle. It is measured in seconds and is the reciprocal of the frequency.

Frequency formula

\[f = \frac{1}{T}\]

The frequency is the reciprocal of the period.

Period formula

\[T = \frac{1}{f}\]

The period is the reciprocal of the frequency.

Angular frequency

In addition to the regular frequency, the angular frequency ω (omega) is often used in engineering calculations. It represents the phase change per unit time in radians per second.

Angular frequency formula

\[\omega = 2\pi f = \frac{2\pi}{T}\]

The angular frequency is 2π times the regular frequency.

Practical applications

Electrical engineering

AC power systems
Motor control
Filter design
Resonance calculations

Electronics

Oscillator circuits
Clock generation
Signal processing
Timer circuits

Communications

Radio frequencies
Carrier waves
Modulation
Bandwidth calculations

Unit conversions

Common frequency units

1 kHz = 1,000 Hz

1 MHz = 1,000,000 Hz

1 GHz = 1,000,000,000 Hz

1 ms = 0.001 s

1 µs = 0.000001 s

1 ns = 0.000000001 s

Design notes

Practical considerations

Sampling rate: Must be at least 2× the highest signal frequency (Nyquist theorem)
Clock accuracy: Crystal oscillators provide precise timing references
Harmonic content: Non-sinusoidal signals contain multiple frequencies
Bandwidth: Signal bandwidth determines the frequency range occupied
Resonance: LC circuits resonate at f = 1/(2π√LC)
Phase relationships: Multiple frequencies can have complex phase interactions

AC functions