Dodecagon (12-gon) Calculator

Calculator and formulas for regular dodecagons

Dodecagon Calculator

Regular Dodecagon

A regular dodecagon has 12 equal sides and 12 equal interior angles (150°). It corresponds to the hours on a clock.

Enter known parameter
Which parameter is known?
Value of the selected parameter
Calculation Results
Side length a:
Perimeter P:
Area A:
Diagonal d2:
Diagonal d3:
Diagonal d4:
Diagonal d5:
Diagonal d6:
Inner radius ri:
Outer radius ra:

Regular Dodecagon

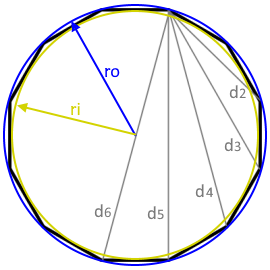
Dodekagon

The diagram shows a regular dodecagon with all relevant parameters.
All 12 sides are equal in length, all interior angles measure 150°.

Properties of a regular dodecagon

A regular dodecagon (dodecagon) is a highly symmetric geometric object:

  • 12 equal sides: All side lengths are identical
  • 12 equal angles: Each interior angle is exactly 150°
  • Sum of angles: 10 × 180° = 1800°
  • Clock analogy: 12 positions like hours on a clock
  • Central angle: 360°/12 = 30° per segment
  • Constructibility: Can be constructed with compass and straightedge

The dodecagon and the clock

The regular dodecagon has a natural connection to timekeeping:

Clock hand positions
  • 12 hours correspond to 12 vertices
  • Central angle 30° = 1 hour
  • Hour hand rotates 30° per hour
  • Natural orientation aid
Navigation relation
  • Compass rose with 12 main directions
  • 30° intervals for navigation
  • Historic wind rose division
  • Maritime and terrestrial orientation

Construction and mathematical properties

The regular dodecagon shows interesting mathematical properties:

Classical construction
  • Constructible with compass and straightedge
  • Via triple and quadruple division of the circle
  • Combination of triangle and quadrilateral
  • Central angle: 360°/12 = 30°
Mathematical values
  • sin(30°) = 1/2, cos(30°) = √3/2
  • Simple trigonometric relations
  • Connections to √2 and √3
  • Integer divisibility of angle sum

Applications of the regular dodecagon

Regular dodecagons have a wide range of practical applications:

Clocks & timekeeping
  • Watch faces and clock cases
  • Tower clock designs
  • Chronometers and precision watches
  • Decorative clocks and wall clocks
Architecture & art
  • Stained glass windows and rosettes
  • Dome constructions
  • Garden layouts and fountains
  • Decorative floor patterns
Navigation & orientation
  • Compass roses and wind charts
  • Nautical navigation instruments
  • Astronomical measuring devices
  • Surveying and geodetic techniques
Engineering & industry
  • Mechanical engineering: gears and couplings
  • Electrical engineering: connectors
  • Automotive: rims and wheels
  • Optics: prisms and lens systems

Formulas for the regular dodecagon (dodecagon)

Area A
\[A = 3(2 + \sqrt{3}) \cdot a^2 \approx 11.196 \cdot a^2\]

Combination of squares and triangles

Perimeter P
\[P = 12 \cdot a\]

Simple: 12 times the side length

Diagonal d₂
\[d_2 = \frac{\sqrt{6} + \sqrt{2}}{2} \cdot a \approx 1.932 \cdot a\]

Shortest diagonal

Diagonal d₃
\[d_3 = (\sqrt{3} + 1) \cdot a \approx 2.732 \cdot a\]

With √3 and 1

Diagonal d₄
\[d_4 = \frac{3\sqrt{2} + \sqrt{6}}{2} \cdot a \approx 3.347 \cdot a\]

Combination of √2 and √6

Diagonal d₅ (Height h)
\[d_5 = h = (2 + \sqrt{3}) \cdot a \approx 3.732 \cdot a\]

Longest diagonal = height

Diagonal d₆
\[d_6 = (\sqrt{2} + \sqrt{6}) \cdot a \approx 3.864 \cdot a\]

Maximum diagonal

Inner circle radius rᵢ
\[r_i = \frac{(2 + \sqrt{3}) \cdot a}{2} \approx 1.866 \cdot a\]

Half the height d₅

Circumcircle radius rₐ
\[r_a = \frac{\sqrt{6} + \sqrt{2}}{2} \cdot a \approx 1.932 \cdot a\]

Equals diagonal d₂

Calculation example for a dodecagon

Given
Side length a = 10

Find: all properties of the regular dodecagon

1. Compute base measures
\[P = 12 \times 10 = 120\] \[A = 11.196 \times 100 = 1119.6\]

Perimeter and area

2. Compute radii
\[r_a = 1.932 \times 10 = 19.32\] \[r_i = 1.866 \times 10 = 18.66\]

Circumradius and inradius

3. All diagonals
d₂ = 1.932 × 10 = 19.32 d₃ = 2.732 × 10 = 27.32 d₄ = 3.347 × 10 = 33.47
d₅ = h = 3.732 × 10 = 37.32 d₆ = 3.864 × 10 = 38.64

All five distinct diagonal lengths

4. Full summary
Side length a = 10.00 Perimeter P = 120.00 Area A = 1119.60 Height h = 37.32
Circumradius = 19.32 Inradius = 18.66 Interior angle = 150° Central angle = 30°

Complete characterization of the regular dodecagon

The regular dodecagon in theory and practice

The regular dodecagon occupies a special place among polygons, as it represents a perfect balance between geometric simplicity and practical applicability. Its connection to our time system and navigation makes it one of the culturally significant geometric shapes.

Mathematical elegance and construction

The mathematical properties of the regular dodecagon show particular elegance:

  • Simple construction: As a 3×4 or 4×3 division of the circle very accessible
  • Known trigonometric values: sin(30°) = 1/2, cos(30°) = √3/2
  • Combinatorial properties: Combines properties of triangle and quadrilateral
  • Symmetry: 12-fold rotational and reflection symmetry
  • Divisibility: Evenly divisible by 2, 3, 4 and 6

Cultural and practical importance

The practical importance of the dodecagon is evident in many areas:

Time systems

From ancient sundials to modern chronometers - the dodecagon shapes our sense of time through the 12-hour division of the day.

Navigation

Compass roses and navigation instruments use the 12-part structure for precise direction in 30° steps.

Architecture

Stained glass windows, domes and garden designs use the dodecagon as a harmonious design element.

Engineering

Mechanical and electrical engineering value the even distribution for gears, connectors and rotational components.

Modern applications and future perspectives

In modern technology the dodecagon gains new relevance:

  • CAD/CAM systems: Standard shape for rotationally symmetric components and tools
  • Robotics: 12-part sensor and actuator arrays for omnidirectional movement
  • Optics: Aperture designs and prism systems use 12-fold symmetry
  • Nannotechnology: Molecular structures with 12-fold symmetry
  • Energy technology: Wind and solar layouts with optimal spatial distribution
Summary

The regular dodecagon combines mathematical elegance with cultural importance and practical applicability. Its relation to time and navigation, easy constructibility and harmonious proportions make it a timeless geometric shape. From ancient sundials to modern high-precision instruments, the dodecagon demonstrates the lasting relevance of classical geometry in a technologized world.

Is this page helpful?            
Thank you for your feedback!

Sorry about that

How can we improve it?

More polygons

Triangle • Square • Pentagon • Hexagon • Heptagon • Octagon • Nonagon • Decagon • Hendecagon • Dodecagon • Hexadecagon • N-Gon • Polygon ring • Concave hexagon • Axial Symmetric Pentagon • Irregular, stretched Hexagon • Irregular, stretched Octagon • Pentagram • Hexagram • Octagram • Star of Lakshmi