Pentagram Calculator
Calculator and formulas for the five-pointed star of the Golden Ratio
Pentagram Calculator
The Pentagram
A pentagram is a five-pointed star with the Golden Ratio (Φ ≈ 1.618) as its fundamental principle. Symbol of perfection.
Pentagram structure
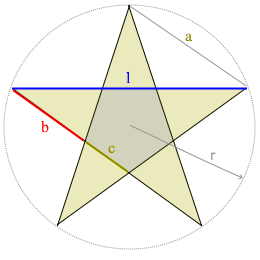
The pentagram perfectly embodies the Golden Ratio (Φ).
Four different lengths: l, a, b, c - all in ratio Φ.
|
|
The Pentagram: Star of perfection
The pentagram is one of the most fascinating geometric forms of humanity:
- Five-pointed star: Constructed from a regular pentagon
- Golden Ratio: Φ ≈ 1.618 permeates all proportions
- Four lengths: l, a, b, c in perfect harmonic sequence
- Universal symbol: Sign of perfection in all cultures
- Mathematical elegance: Geometry and algebra united
- Spiritual meaning: Five elements, five senses, human in cosmos
The Golden Ratio (Φ) in the Pentagram
The pentagram is the geometric embodiment of the Golden Ratio:
Φ definition
- Divine proportion
- Irrational number
- Self-similar properties
- Φ² = Φ + 1
Length ratios
- Total length to pentagon side
- Pentagon side to long chord
- Long chord to short chord
- Harmonic chain of Φ ratios
Symbolism and cultural meaning
The pentagram is one of the most powerful symbols in human history:
Ancient traditions
- Pythagoreans: Symbol of perfection
- Greeks: Pentagramma, sacred geometry
- Romans: Venus star, sign of love
- Celts: Druid star, nature connection
Universal meanings
- Five elements: Fire, water, earth, air, ether
- Human: Head, four limbs in the cosmos
- Senses: Sight, hearing, smell, taste, touch
- Perfection: Harmony and balance
Applications of the pentagram
The pentagram finds diverse applications in science, art and culture:
Nature & biology
- Flowers with 5 petals (roses, apple blossoms)
- Starfish and sea urchins
- Crystal structures (quasicrystals)
- Molecular geometry
Art & architecture
- Renaissance art (Da Vinci, Dürer)
- Church architecture and rose windows
- Modern logo design
- Jewelry and ornaments
National symbols
- Flags (USA, China, EU, many others)
- Military badges and orders
- State emblems and coats of arms
- International organizations
Modern technology
- Computer graphics and 3D modeling
- Algorithm development
- Architecture software (CAD)
- Artificial intelligence (pattern recognition)
Formulas for the pentagram
Golden Ratio Φ
Fundamental constant of the pentagram
Side length a
Pentagon side length
Total length l
Point to point of the star
Long chord b
Diagonal of the inner pentagon
Short chord c
Side of the inner pentagon
Perimeter U
10 outer edges of the star
Area A
Total area of the five-pointed star
Circumradius r
Radius of the circumscribed circle
Calculation example for a pentagram
Given
Find: All properties of the five-pointed star
1. Φ calculations
Golden ratio relationships
2. Additional lengths
Short chord and perimeter
3. Verify Φ ratios
All ratios perfectly match the Golden Ratio
4. Complete pentagram
The perfect pentagram - geometry of the Golden Ratio
The pentagram: Star of the Golden Ratio
The pentagram is far more than just a geometric symbol - it is the perfect embodiment of the Golden Ratio and thus one of the most harmonious forms in mathematics. As a five-pointed star, it unites geometric perfection with spiritual symbolism and shows how mathematics and mysticism, science and art, can converge in a single elegant form.
The Golden Ratio: God's geometry
The pentagram is the geometric manifestation of the Golden Ratio:
- Φ = (1+√5)/2 ≈ 1.618: The divine proportion permeates every line
- Harmonic chain: l:a = a:b = b:c = Φ
- Self-similarity: Each smaller pentagon reproduces the same ratios
- Irrational beauty: Φ is irrational, yet creates perfect harmony
- Fibonacci connection: lim(Fn+1/Fn) = Φ for Fibonacci numbers
- Spiral geometry: Golden spirals arise naturally from pentagon structures
From Pythagoras to Leonardo: A mathematical journey
The history of the pentagram is the history of mathematics itself:
Ancient discoveries
The Pythagoreans discovered the pentagram as a symbol of perfection and recognized in it the first proof of irrational numbers - a discovery that shattered their worldview.
Renaissance revolution
Leonardo da Vinci, Albrecht Dürer and other Renaissance masters used the pentagram to manifest divine geometry in art and architecture.
Modern mathematics
Today we understand the pentagram as a window to Galois theory, group theory and complex analysis - it connects elementary geometry with the highest mathematics.
Scientific relevance
From quasicrystals to molecular structures - the pentagram and Golden Ratio structure nature at all levels.
Universal symbolism: The humanity symbol
The pentagram transcends cultural boundaries:
- Human in cosmos: Da Vinci's Vitruvian Man shows the fivefold symmetry of the body
- Five elements: The basic building blocks of reality in almost all cultures
- Five senses: Our perception channels to the world
- Venus cycle: Venus's planetary orbit draws a pentagram in the sky
- Biological quintuple: Five-petaled flowers, five-rayed starfish
- National symbols: Stars on flags represent ideals and values
Modern applications: From lab to screen
The pentagram shapes our modern world:
Science and technology
Quasicrystal research, molecular design, computer graphics algorithms and AI pattern recognition use pentagonal symmetries for groundbreaking innovations.
Design and architecture
From Apple logos to Pentagon buildings - the pentagram creates brand recognition and aesthetic harmony in modern design.
Therapeutic applications
Art therapy, mandala meditation and architectural psychology use the harmonizing effect of pentagonal forms on the human psyche.
Cultural continuity
As a universal symbol for perfection and harmony, the pentagram connects ancient wisdom with modern scientific insights.
Summary
The pentagram is the geometric poetry of the universe - a form in which the deepest mathematical truths unite with the human longing for harmony and perfection. As a living manifestation of the Golden Ratio, it embodies the paradox that irrational numbers can lead to rational beauty. From the ancient Pythagoreans, who recognized in it the secrets of numbers, to modern scientists who apply its principles in quasicrystals and algorithms, the pentagram remains timeless proof that mathematics is not just calculation, but the language of beauty, bridge between mind and feeling, window to cosmic order. In a world full of complexity, the five-pointed star reminds us that true elegance lies in simplicity - and that the most beautiful truths are often the simplest ones: Φ.
|
|
|
|