Octagon (8-gon) Calculator
Calculator and formulas for regular octagons
Octagon Calculator
Regular Octagon
A regular octagon has 8 equal sides and 8 equal interior angles (135°). 8 = 2³ (power of 2).
Regular Octagon
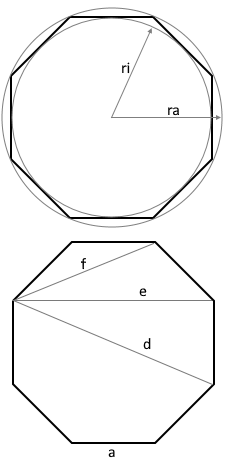
The diagram shows a regular octagon with all relevant parameters.
All 8 sides are equal in length, all interior angles measure 135°.
|
|
Properties of a regular octagon
A regular octagon is one of the most symmetric geometric forms:
- 8 equal sides: All side lengths are identical
- 8 equal angles: Each interior angle measures exactly 135°
- Sum of angles: 6 × 180° = 1080°
- Power of 2: 8 = 2³ - special properties
- Central angle: 360°/8 = 45° per segment
- Construction: Easy to construct
The octagon and binary systems
The regular octagon benefits from its power-of-2 property:
2³ properties
- 8 = 2³ (3rd power of 2)
- Binary: 1000 (4 bits)
- Octal system: base 8
- Easy halving possible
Divisibility properties
- Divisible by: 1, 2, 4, 8
- Square (4-gon) as half
- 45° angles are exactly representable
- Stop sign form (known worldwide)
Geometric elegance and construction
The regular octagon shows special geometric elegance:
Simple construction
- Constructible with compass and straightedge
- 45° angles are exactly constructible
- Central angle: 360°/8 = 45°
- √2 relationships in all formulas
Mathematical values
- sin(45°) = cos(45°) = √2/2
- tan(45°) = 1
- sin(22.5°) = √(2-√2)/2
- All values exactly representable
Applications of the regular octagon
Regular octagons have broad practical applications:
Traffic & safety
- Stop signs (internationally standardized)
- Traffic signs and warning boards
- Safety and information signs
- Industrial marking
Architecture & construction
- Octagonal towers and pavilions
- Windows and skylights
- Tiles and floor coverings
- Garden pavilions and gazebos
Technology & industry
- Mechanical engineering components
- Screw heads and nuts
- Bearings and couplings
- Precision tools
Games & design
- Board game elements
- Puzzles and brain games
- Graphic design and logos
- Decorative art objects
Formulas for the regular octagon
Area A
Elegant formula with √2
Perimeter P
Simple: 8 times the side length
Long diagonal d
Diameter of the octagon
Medium diagonal e
Double inner radius
Short diagonal f
Shortest of the three diagonals
Circumradius rₐ
Half long diagonal
Inradius rᵢ
Apothem of the octagon
Alternative area formula
Via circumradius
Calculation example for an octagon
Given
Find: All properties of the regular octagon
1. Calculate basic measures
Perimeter and area
2. Calculate radii
Circumradius and inradius
3. All three diagonals
Short, medium and long diagonal
4. Complete summary
The perfect octagon for traffic signs and architecture
The regular octagon: Symbol of order
The regular octagon is probably the best known of all polygons, since it is perceived daily millions of times around the world as a stop sign. But behind this everyday nature lies a mathematically elegant form with special properties and diverse applications.
The power of eight: 2³ and its significance
The number 8 as the third power of 2 gives the octagon special mathematical elegance:
- Binary perfection: 8 = 2³ corresponds to exactly 3 bits in digital systems
- 45° geometry: Central angle 45° = 90°/2 - perfectly constructible
- √2 relationships: All formulas contain √2 as an elegant factor
- Stop sign universality: Recognized worldwide as "STOP"
- Architectural tradition: Thousands of years of use in construction
The stop sign: Global symbol of order
The most famous application of the octagon is the international stop sign:
Historical development
Developed in 1915 in the USA, the octagonal stop sign prevailed due to its unique shape. No other traffic sign has this characteristic 8-sided form.
Psychological effect
The 8 corners and red color immediately signal "danger" and "stop". Even in poor visibility, the octagonal silhouette is immediately recognizable.
International standardization
The Vienna Convention on Road Signs made the octagonal stop sign the worldwide standard. Form before language!
Practical advantages
Recognizable from behind, wind and weather stable, easy to produce and mount. The perfect connection of geometry and function.
Architectural tradition and modern applications
The octagon has a rich architectural history and modern applications:
- Classical architecture: Baptisteries, chapels and central buildings
- Islamic art: Octagonal patterns in mosques and palaces
- Modern architecture: Residential towers, office buildings and pavilions
- Garden and landscape architecture: Gazebos, fountains and observation towers
- Industrial design: Machine components, screws and connecting elements
- Digital world: Icons, logos and user interface elements
Mathematical elegance and practical calculations
The mathematical relationships in the octagon show special beauty:
√2 family
All octagon formulas are based on √2 and its powers. The area 2a²(1+√2) shows the elegant connection between side length and root expressions.
Three diagonal types
Short (f), medium (e) and long diagonal (d) stand in harmonic relationships and enable versatile constructive applications.
45° symmetry
The 45° central angle makes the octagon one of the most construction-friendly polygons. Right angles can be exactly halved.
Practical calculability
Despite the √2 expressions, all values are well approximable with simple calculators and practically usable.
Summary
The regular octagon unites mathematical elegance with practical functionality like hardly any other geometric form. As a stop sign, it is probably the best known polygon in the world and saves lives daily through its clear recognizability. Its properties as 2³ make it ideal for technical applications, while the √2 relationships reveal mathematical beauty. From ancient baptisteries to modern traffic systems, the octagon shows how geometry can connect culture, safety and aesthetics. It stands as a symbol for order, safety and the perfect balance between simplicity and elegance.
|
|
|
|