Pentagon (5-gon) Calculator
Calculator and formulas for regular pentagons
Pentagon Calculator
Regular Pentagon
A regular pentagon has 5 equal sides and 5 equal interior angles (108°). Closely connected to the golden ratio φ.
Regular Pentagon
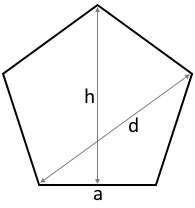
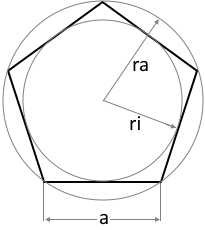
The diagrams show a regular pentagon with all relevant parameters.
All 5 sides are equal in length, all interior angles measure 108°.
|
|
Properties of a regular pentagon
A regular pentagon is one of the most mathematically fascinating geometric forms:
- 5 equal sides: All side lengths are identical
- 5 equal angles: Each interior angle measures exactly 108°
- Sum of angles: 3 × 180° = 540°
- Golden ratio: φ = (1+√5)/2 ≈ 1.618
- Central angle: 360°/5 = 72° per segment
- Five-fold symmetry: Widespread in nature
The pentagon and the golden ratio
The regular pentagon is inseparably connected to the golden ratio φ:
Golden ratios
- Diagonal : Side length = φ ≈ 1.618
- φ = (1 + √5)/2 (golden ratio)
- Diagonal = a · φ
- All formulas contain √5
Pentagram magic
- Five-pointed star in the pentagon
- Infinitely many golden ratios
- Self-similar structures
- Symbol of perfection
The pentagon in nature
Five-fold symmetry is a fundamental principle of living nature:
Plant world
- Five-petaled flowers (roses, apple, cherry)
- Five-fold leaf arrangement
- Starfish and sea urchins
- Fruits (apple cross-section)
Biological structures
- Human body (5 fingers, 5 toes)
- Fibonacci spirals in flowers
- Crystal structures (quasicrystals)
- Viral capsids (icosahedra)
Applications of the regular pentagon
Regular pentagons find diverse applications:
Architecture & politics
- The Pentagon (US Department of Defense)
- Five-sided buildings and towers
- Historical fortresses
- Modern architectural elements
Art & design
- Pentagram in art and religion
- Graphic design and logos
- Decorative art objects
- Golden ratio designs
Games & puzzles
- Strategy games with 5-sided fields
- Puzzles and brain games
- Board game elements
- Five-sided dice
Science & technology
- Quasicrystals (Nobel Prize 2011)
- Molecular chemistry
- Optical systems
- Nanotechnology
Formulas for the regular pentagon
Area A
Elegant formula with √5 and φ
Perimeter P
Simple: 5 times the side length
Diagonal d
Golden ratio φ = (1+√5)/2
Height h
Sum of circumradius and inradius
Circumradius rₐ
With sin(36°) = √(10-2√5)/4
Inradius rᵢ
Apothem of the pentagon
Side length (from diagonal)
Inverse golden ratio
Pentagram relationship
Inner star of the pentagram
Calculation example for a pentagon
Given
Find: All properties of the regular pentagon
1. Calculate basic measures
Perimeter and area
2. Golden ratio
Diagonal and golden ratio
3. Radii and height
Circumradius, inradius and height
4. Golden magic
The pentagon reveals the secrets of the golden ratio φ
The regular pentagon: Golden secrets
The regular pentagon is probably the most mysterious and fascinating of all polygons. It connects mathematics, nature, art and mysticism in a unique way and reveals the deepest secrets of the golden ratio. No other geometric form shows so clearly the hidden harmony of the universe.
The golden ratio: φ = (1+√5)/2 ≈ 1.618
The pentagon is the geometric home of the golden ratio φ (Phi):
- Diagonal to side: Ratio d:a = φ:1 (the golden ratio)
- Pentagram magic: The five-pointed star contains infinitely many golden ratios
- Self-similarity: Every pentagon in the pentagram stands in golden proportion
- Fibonacci connection: lim(Fn+1/Fn) = φ for Fibonacci numbers
- Divine proportion: The "divine proportion" of Renaissance artists
The pentagram: Symbol of perfection
The five-pointed star in the pentagon holds mathematical wonders:
Infinite nesting
Every point of the pentagram forms another small pentagon. This structure can be continued infinitely - a fractal property.
Mystical meaning
The pentagram was already sacred to the Pythagoreans. It symbolized health and was used as a sign of recognition.
Golden cascade
Every line segment in the pentagram divides another in the golden ratio. This creates 4 different lengths in harmonic proportions.
Constructive elegance
The pentagon can be constructed with compass and straightedge alone - a masterpiece of ancient geometry.
The five in nature: Universal life principle
Five-fold symmetry permeates living nature at all levels:
- Human body: 5 senses, 5 fingers, 5 toes - humans as pentagrams
- Flower world: Countless flowers show 5-fold symmetry (roses, apple, cherry, hibiscus)
- Marine life: Starfish and sea urchins as living pentagons
- Quasicrystals: Nobel Prize 2011 for impossible 5-fold crystal symmetry
- Viral shells: Icosahedra with 20 triangular and 12 pentagonal faces
- Botany: Phyllotaxis - leaf arrangement following Fibonacci spirals
Cultural and symbolic meaning
The pentagon and pentagram have deep cultural roots:
Antiquity and Middle Ages
Among the Pythagoreans, a symbol of health and perfection. In the Middle Ages, protection against evil spirits. In alchemy, symbol for ether.
Renaissance
Leonardo da Vinci and other artists consciously used the golden ratio for harmonious proportions in art and architecture.
Modern times
The Pentagon as building of the US Department of Defense. Flags with pentagrams (USA, China, EU). Symbol of power and authority.
Science today
Quasicrystals, fullerenes, DNA structure - the pentagon remains central in modern science.
Summary
The regular pentagon is far more than just a geometric form - it is a key to understanding the hidden harmony of the universe. Through its inseparable connection to the golden ratio φ, it reveals mathematical truths ranging from quantum physics to art. Omnipresent in nature, symbolically charged in culture, and mathematically of inexhaustible elegance, the pentagon stands as living proof that beauty and truth, nature and mathematics are inseparably connected. It reminds us that behind the apparent complexity of the world, simple, universal principles work - and that these principles are of timeless beauty.
|
|
|
|