Calculate square
Calculator and formulas for the perfect geometric shape
Square calculator
The square
A square is the perfect geometric form with four equal sides and right angles.
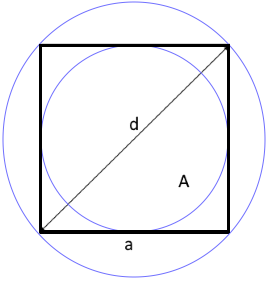
Square with circles
Square properties
Perfection: Four equal sides, four 90° angles, √2 diagonals
The square with incircle and circumcircle.
Perfect symmetry in four axes.
|
|
The square: perfection of geometric form
The square embodies geometric completion like no other shape:
- Four equal sides: Perfect uniformity in all directions
- Four right angles: Each angle exactly 90°
- √2 diagonals: d = a × √2 ≈ 1.414 × a
- Four symmetry axes: Two perpendicular bisectors + two diagonals
- Incircle and circumcircle: Circumcircle area = 2 × incircle area
- Maximum efficiency: Largest area for a given perimeter
Geometric properties of the square
The distinct properties of the square make it a foundational geometric shape:
Symmetry properties
- Four axes of symmetry (record among quadrilaterals)
- Point symmetry about the center
- 90°, 180°, 270° rotational symmetry
- Diagonals bisect each other perpendicularly
Circle relations
- Incircle radius r_i = a/2
- Circumcircle radius r_u = d/2 = a√2/2
- Circumcircle area = 2 × incircle area
- Circles touch at midpoints of sides
Mathematics of the perfect square
The mathematical relations of the square are elegant and fundamental:
√2 relations
- Diagonal d = a × √2 ≈ 1.414 × a
- √2 ≈ 1.41421356... (irrational number)
- Circumcircle radius r_u = a/√2
- Fundamental role in number theory
Simple formulas
- Area A = a² (squaring!)
- Perimeter U = 4a
- All other parameters computable from any given parameter
- Basis for coordinate systems
Applications of the square
Squares are omnipresent in technology, culture and nature:
Architecture & construction
- Floor planning and space division
- Tiles, pavers and floor coverings
- Windows, doors and structural elements
- Modular building systems
Digital world
- Pixels in screens and displays
- QR-codes and digital barcodes
- Game design (Minecraft, Tetris)
- User interface elements
Art & design
- Mondrian and geometric abstraction
- Bauhaus design and modernism
- Logo design with clear shapes
- Graphic grids and layouts
Science & technology
- Crystal lattices and material science
- Coordinate systems in mathematics
- Circuit layout design in electronics
- Image processing and computer vision
Formulas for the square
Area A
The classic squaring of the side length
Perimeter U
Four equal sides summed
Diagonal d
The famous √2 relationship
Side length a (inverse formulas)
Back-calculations from different parameters
Incircle radius r_i
Half the side length
Circumcircle radius r_u
Half the diagonal
Incircle area A_i
Circle area with incircle radius
Circumcircle area A_u
Circle area with circumcircle radius (= 2 × A_i)
Worked example for a square
Given
Find: All parameters of the square
1. Base parameters
Area, perimeter and diagonal
2. Circle radii
Incircle and circumcircle radii
3. Circle areas
Incircle and circumcircle area (A_u = 2 × A_i)
4. Complete square
The perfect square - geometric completion in pure form!
The square: cornerstone of geometry and symbol of perfection
The square has stood for millennia as a symbol of perfection, order and mathematical completion. With four equal sides and right angles it embodies the essence of geometric harmony and forms the foundation for countless mathematical concepts - from the Pythagorean theorem to modern digital image processing.
The mathematical completion of the square
The square captivates through its mathematical elegance and simplicity:
- Perfect equality: Four identical sides and four 90° angles
- √2 constant: Diagonal = side × √2 (fundamental irrational number)
- Maximum symmetry: Four axes of symmetry - more than any other quadrilateral
- Quadratic function: Area = a² gives the name "squaring"
- Circle relations: Circumcircle area = 2 × incircle area (elegant doubling)
- Tessellation: Perfect gapless tiling of the plane
The square in cultural history
Culturally and philosophically the square has gained deep significance:
Ancient philosophy
Plato saw the square as the embodiment of earth and stability. The four corners represented the four elements and directions.
Religious symbolism
In many cultures the square symbolizes the material, earthly realm - contrasted with the spiritual circle. Squaring the circle became a symbol of impossible completion.
Architectural history
From Egyptian pyramids to Roman forums to modern city plans - the square has structured human spaces for millennia.
Modern abstraction
Mondrian's compositions and Malevich's "Black Square" revolutionized art through radical geometric reduction.
Technological revolution through squares
The digital revolution is fundamentally based on square structures:
- Pixel revolution: Every screen consists of millions of square pixels
- QR-codes: Square information encoding revolutionizes mobile communication
- Minecraft phenomenon: Square blocks create infinite virtual worlds
- Circuit design: Integrated circuits use square layouts for efficiency
- Image processing: Convolution filters operate with square kernels
- Machine learning: Square matrices are fundamental for neural networks
The square in nature and science
Although less common in nature than circles and spirals, squares appear in special contexts:
Crystallography
Many minerals crystallize in cubic (three-dimensional square) systems. Salt and pyrite show square symmetries.
Physical laws
The inverse-square law (gravitation, electromagnetism) shows how square relations are fundamental in physics.
Biology
Plant cells and some microorganisms display square structures. Checkerboard flowers have square patterns.
Astronomy
Coordinate systems for sky mapping use square grids. CCD sensors in telescopes have square pixel arrays.
Future perspectives of square geometry
The square remains relevant for future technologies:
- Quantum computing: Qubit arrays in square grids for quantum error correction
- Metamaterials: Square unit cells for tailored optical properties
- Smart cities: Square blocks optimize traffic and infrastructure
- 3D printing: Voxels (3D pixels) as cubic building blocks for complex structures
- Blockchain: Square hash functions secure digital transactions
- AR/VR: Square markers and tracking systems for immersive experiences
Summary
The square stands as a timeless symbol of perfection, order and mathematical completion. From ancient pyramids to medieval cloisters to modern screens - this simple shape with four equal sides and right angles has shaped human civilization. In our digital age the square gains new meaning: pixels structure our visual perception, QR-codes revolutionize communication, and square-based algorithms drive artificial intelligence. The square reminds us that true elegance often lies in simplicity - four lines, four angles, infinite possibilities. It embodies the pursuit of perfection and remains a fundamental building block of our geometric world.
|
|
|
|