Elongated Square Pyramid Calculator
Calculator and formulas for an elongated square pyramid (Johnson solid J8)
Elongated Square Pyramid Calculator
The Elongated Square Pyramid
The elongated square pyramid is a Johnson solid (J8) with 4 triangular faces and 4 square faces.
Johnson Solid J8 Properties
The elongated pyramid: Square pyramid combined with square prism
Elongated Square Pyramid Structure
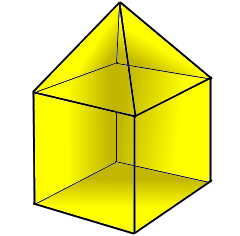
The elongated pyramid with square base.
Johnson solid J8.
|
|
What is an elongated square pyramid?
The elongated square pyramid is a fascinating Johnson solid:
- Definition: Square pyramid combined with square prism
- Johnson solid: J8 in the classification
- Triangular faces: 4 congruent equilateral triangles
- Square faces: 4 congruent squares
- Base: 1 square base
- Edges: 12 edges (all equal length)
Geometric Properties of the Elongated Square Pyramid
The elongated square pyramid shows remarkable geometric properties:
Basic Parameters
- Triangular faces: 4 equilateral triangles
- Square faces: 4 congruent squares
- Square base: 1 square base
- Vertices: 9 vertices total
Special Properties
- Square symmetry: 4-fold rotational symmetry
- Orthogonal structure: Right angles everywhere
- Uniform edges: All edges equal length
- Convex: No concave edges or vertices
Mathematical Relationships
The elongated square pyramid follows elegant square laws:
Volume Formula
Elegant formula with √2 relationship. Simple but precise.
Surface Area Formula
5 squares plus 4 triangles. Contains √3 factor.
Applications of the Elongated Square Pyramid
Elongated square pyramids find applications in various fields:
Architecture & Construction
- Square tower designs
- Modern roof structures
- Architectural spires
- Building elements
Science & Technology
- Crystal structures
- Molecular geometry
- Optical components
- Engineering applications
Education & Teaching
- Square geometry studies
- 3D visualization
- Johnson solid education
- Mathematical modeling
Art & Design
- Geometric sculptures
- Square-based art
- Modern design elements
- Architectural details
Elongated Square Pyramid Formulas
Volume (V)
Volume combining square prism and pyramid
Surface Area (S)
5 squares plus 4 equilateral triangles
Height (h)
Height with √2 factor for square geometry
Johnson Solid
8th Johnson solid in the classification
Elongated Square Pyramid Parameters
4 equilateral △
4 squares □
1 square ■
9 vertices
12 edges
All properties follow from the square symmetry and √2 relationships
Calculation Example for an Elongated Square Pyramid
Given
Find: All properties of the elongated square pyramid
1. Volume Calculation
For a = 10:
\[V = \left(1+\frac{\sqrt{2}}{6}\right) \cdot 10^3\] \[V ≈ 1.2357 \cdot 1000\] \[V ≈ 1235.7\]The volume is approximately 1235.7 cubic units
2. Surface Area Calculation
For a = 10:
\[S = (5+\sqrt{3}) \cdot 10^2\] \[S ≈ 6.732 \cdot 100\] \[S ≈ 673.2\]The surface area is approximately 673.2 square units
3. Height Calculation
For a = 10:
\[h = \left(1+\frac{\sqrt{2}}{2}\right) \cdot 10\] \[h ≈ 1.7071 \cdot 10\] \[h ≈ 17.071\]The height is approximately 17.071 length units
4. The Square Structure
The elongated square pyramid with perfect square symmetry
The Elongated Square Pyramid: Square Symmetry Excellence
The elongated square pyramid represents one of the most elegant examples of square symmetry in three-dimensional geometry. By combining a square pyramid with a square prism, this Johnson solid creates a perfect balance between the angular precision of right angles and the smooth curves of triangular faces. The mathematical beauty lies in the elegant √2 relationships that govern all proportions, reflecting the fundamental geometry of the square. As Johnson solid J8, it demonstrates how simple geometric extension can transform basic shapes into sophisticated architectural and mathematical structures.
The Geometry of Square Perfection
The elongated square pyramid showcases the beauty of square-based geometry:
- Square base: Perfect right-angled foundation
- 4-fold symmetry: 90° rotational symmetry
- Orthogonal structure: All angles are either 60° or 90°
- Johnson solid: J8 in the classical classification
- Mixed faces: Squares and equilateral triangles in harmony
- Uniform edges: All edges have the same length
- Structural stability: Excellent load-bearing properties
Mathematical Elegance
Square Root Harmony
The formulas elegantly incorporate √2 and √3 factors, showing how square and triangular geometries naturally complement each other in three-dimensional space.
Orthogonal Precision
The perfect right angles of the square base create a stable foundation that extends naturally into the triangular pyramid section.
Architectural Excellence
The square base makes this form ideal for construction and engineering applications where stability and right-angle orientation are crucial.
Geometric Balance
The balance between the stable square prism and the dynamic triangular pyramid creates a visually compelling and mathematically satisfying form.
Summary
The elongated square pyramid embodies the perfect marriage of mathematical precision and geometric beauty. Its elegant formulas, governed by √2 relationships and square symmetry, make it both theoretically fascinating and practically useful. As Johnson solid J8, it bridges the gap between elementary square geometry and sophisticated three-dimensional design. From ancient architectural forms to modern engineering applications, this remarkable polyhedron continues to demonstrate the power of square-based symmetry in creating structures that are both beautiful and functional. Its combination of stability, elegance, and mathematical precision makes it a cornerstone of geometric understanding and practical application.
|
|
|
|